2D AND 3D QSAR STUDIES ON THIAZOLES AND OXADIAZOLES HAVING ANTIPLATELET ACTIVITY BY MULTIPLE REGRESSIONS FORWARD, PRINCIPLE COMPONENT REGRESSION FORWARD AND PARTIAL LEAST SQUARE REGRESSION FORWARD METHOD

Research Paper

SGVU Journal of Pharmaceutical Research & Education

 

 

Journal homepage: http://www.gyanvihar.org/researchjournals/

 

2D AND 3D QSAR STUDIES ON THIAZOLES AND OXADIAZOLES HAVING ANTIPLATELET ACTIVITY BY MULTIPLE REGRESSIONS FORWARD, PRINCIPLE COMPONENT REGRESSION FORWARD AND PARTIAL LEAST SQUARE REGRESSION FORWARD METHOD

1. A. Kashid *¹, S. K. Singh¹, P. B. Patil¹, J. Saravanan²

Suresh Gyan Vihar University¹, Mahal Jagatpura, Jaipur – 302017, Rajasthan, India.

PES College of Pharmacy², Bangalore – 560050, Karnataka, India.

Abstract

Thiazole analogues’ antiplatelet action was recently discovered. Principal component analysis, partial least squares, multiple regression, and k-NN MFA 3-Dimensional Simulations of QSAR have been created. Considering the q2 and pred r2 values, either of these models was chosen. Through cross-validation (pred r2) and q2 validation, the chosen model demonstrated a strong intrinsic and extrinsic prognosis for the training-set and test-set dimensions of 63 and 10 analogues respectively. To create correlations between the physical and chemical characteristics of chemicals as well as their platelet inhibition actions and to produce a trustworthy quantitative prediction model, thiazole derivative QSAR analysis has been employed. The best model demonstrated by the 3-Dimensional QSAR analysis was completed using the partial least-square regression-forward technique with a r² value of 0.93, while the best model for the 2-Dimensional QSAR study was reported using the multiple regression-forward methods with a r² value of 0.912 and strong predictive power. Future designs of more effective anticancer congeners may be based on the findings from QSAR investigations.

Keywords: Antiplatelet Action, Thiazole analogs, and 3-Dimensional and 2-Dimensional QSAR.

 

Introduction

The term Quantitative Structure-Activity Relationship (QSAR) refers to a plan for creating computational or quantitative designs It employs a chemometric approach in an effort to find a significant correlation association among structure/function The structure in drug design relates to the characteristics or descriptors of the analogues, and the function of their substituents corresponding to an experimental measure of interaction energy fields endpoint in biology or biochemistry, such as lethality, effectiveness, high affinity, or rate constants. Chemo metric methods involve GA, ANN, PCR, PCA, PLS, MLR, etc. When a property in addition to pharmacological activities is involved, the term “quantitative structure-property relationship” (-QSPR) is often used. Over the course of more than a century, several QSAR techniques have been steadily developed and are indeed statistical inferences tools, notably in the development of medicines and agrochemicals.

By way of Crammers 3-dimensional QSAR and, Vedani’s-fifth, Hopfinger’s -fourth and Free-sixth Wilson’s aspects, approaches had advanced from Hansch and Free-one Wilson’s or 2-dimensional linear free energy correlations. The term “classical” QSAR approaches refer to all one-, two-, and related procedures. Every chemical used ties to the same in the research receptor at the equivalent location. The primary distinction between all of these formalisms, however, is in how each one approaches, depicts, and extracts the quantitative correlations among of properties and potency of the molecules. Due to the opportunity limitations and the reliance on electrostatic, steric, or hydrophobic characteristics

Materials and Methods

The data set for the QSAR investigation includes every synthesized derivative with antioxidant activity. This dataset’s antioxidant activity is described as IC50 digits. Chemically, the structures were created using 2-Dimensional Draw software and V-Life MDS apps then transformed to 3-Dimensional. (V-Life sciences Pvt Ltd Pune). The MMFF 94 force field and Gasteiger Marsili charges were used to single-point optimize each structure until a gradient of 0.001 kcal/A0 was achieved. By using template base alignment, the optimized molecule should be aligned. The table includes the general structures and appropriate replacements.

Figure 1 illustrates a 3–Dimensional representation of the alignment of the GS 1a to GS 1l derivatives using the template base.

 

Figure 2 illustrates a 3–Dimensional representation of the alignment of the GS 2ia to GS 4c derivatives using the template base.

Figure 3 illustrates a 3–Dimensional representation of the alignment of the GS 5ia to GS 7id derivatives using the template base.

 

Figure 4 illustrates a 3–Dimensional representation of the alignment of the GS 8ia to GS 8im derivatives using the template base.

Figure 5 illustrates a 3–Dimensional representation of the alignment of the GS 9ia to Gs 9ii derivatives using the template base.

Sr. No.	Comp. No.	Activity	log	Negative log
1	GS1a	156.19	2.183	-2.183
2	GS1b	164.49	2.206	-2.206
3	GS1c	144.58	2.160	-2.160
4	GS1d	63.68	1.804	-1.804
5	GS1e	97.41	1.988	-1.988
6	GS1f	36.86	1.566	-1.566
7	GS1g	98.54	1.993	-1.993
8	GS1h	206.20	2.304	-2.304
9	GS1i	131.35	2.108	-2.108
10	GS1j	100.33	2.001	-2.001
11	GS1k	187.25	2.272	-2.272
12	GS1l	63.12	1.800	-1.800
13	GS2ia	181.57	2.272	-2.272
14	GS2ib	97.07	1.981	-1.981
15	GS2ic	123.49	2.045	-2.045
16	GS2id	92.35	1.956	-1.956
17	GS2ie	58.22	1.764	-1.764
18	GS2if	120.47	2.071	-2.071
19	GS2ig	124.29	2.118	-2.118
20	GS2ih	13.09	1.107	-1.107
21	GS2ii	32.46	1.439	-1.439
22	GS2ij	62.10	1.823	-1.823
23	GS2ik	25.72	1.465	-1.465
24	GS3a	35.18	1.457	-1.457
25	GS3b	84.18	1.851	-1.851
26	GS3c	11.78	1.065	-1.065
27	GS4a	40.33	1.507	-1.507
28	GS4b	89.18	1.850	-1.850
29	GS4c	13.63	1.238	-1.238
30	GS5ia	131.35	2.019	-2.019
31	GS5ib	17.30	1.230	-1.230
32	GS5ic	106.89	2.023	-2.023
33	GS5id	18.53	1.260	-1.260
34	GS6ie	92.03	1.963	-1.963
35	GS6ia	100.75	2.103	-2.103
36	GS6ib	31.14	1.485	-1.485
37	GS6ic	20.27	1.319	-1.319
38	GS7ia	81.34	1.881	-1.881
39	GS7ib	146.91	2.177	-2.177
40	GS7ic	92.67	1.966	-1.966
41	GS7id	27.19	1.236	-1.236
42	GS8ia	99.85	2.001	-2.001
43	GS8ib	94.54	1.975	-1.975
44	GS8ic	12.65	1.102	-1.102
45	GS8id	97.87	1.992	-1.992
46	GS8ie	93.81	1.963	-1.963
47	GS8if	32.01	1.516	-1.516
48	GS8ig	48.41	1.655	-1.655
49	GS8ih	109.48	2.019	-2.019
50	GS8ii	90.61	1.857	-1.857
51	GS8ij	119.71	2.068	-2.068
52	GS8ik	26.86	1.419	-1.419
53	GS8il	132.64	2.1211	-2.120
54	GS8im	160.51	2.551	-2.551
55	GS9ia	54.51	1.633	-1.633
56	GS9ib	109.19	2.021	-2.021
57	GS9c	25.49	1.418	-1.418
58	GS9id	41.29	1.517	-1.517
59	GS9ie	20.81	1.310	-1.310
60	GS9if	86.64	1.838	-1.838
61	GS9ig	68.25	1.735	-1.735
62	GS9ih	19.32	1.268	-1.268
63	GS9ii	161.04	2.217	-2.217

 

 

Table No- 1 Pharmacological Performance

 

1. Database of Pharmacological Performance for QSAR Interpretation

These novel molecules’ antioxidant activity and structural details are listed in the table, which is crucial for 2D and 3D-QSAR research.

1.1 Computational Specifications

All compound structures were depicted using the 2D-Sketch software (MDS 2020). In MDS, the 2D analogs were transformed into 3D-analogues. Merck Molecular Force Field (MMFF) and charges were used to batch optimize each chemical and reduce its energy consumption.

1.2 2D-QSAR Molecular Simulation

1.2.1 Calculation of Descriptors:

Using the descriptor computation feature included in the MDS technology, the Physico-chemical Parameter, Alignment Independent, may be computed. There are calculated to be close to several hundred descriptions. Using the “delete invariable column tool,” the column that has both zero-value reading and invariability is eliminated.

1.2.2 Assignment of the Parameter

For creating a Statistical model, there are one hundred molecular descriptors accessible. Not every molecular attribute is crucial for figuring out the biological activity. It is necessary to use a variable selection approach, which is crucial in assessing activity, to choose the best subset of the descriptors. The step-by-step forward-backward systemic variable selection approach can be used to pick the variables. The log of the IC50 value, which may be employed as a dependent variable in a QSAR analysis, is created from the IC50 value. Create a separate variable for each additional attribute.

1.2.3 Quantitative Approaches

Statistics are analyzed in to be able to create Statistical simulations by using a subset of variables that have the highest statistical significance in predicting the pharmacology potency using an appropriate statistical approach in conjunction with a variable selection method.

1.2.4 Training and test data readiness:

Two sets, training, and test sets can be created according to a set of data. Template base alignment should be used to align optimized molecules. The table contains the general structures and the relevant replacements.

1.2 3D-QSAR Molecular Simulation:

Training and test- data readiness:

Training and test-set may be created using the 3–Dimensional QSAR data collection. By using template base alignment, the optimized compound must be aligned. The table includes basic structures and the appropriate replacements. Similar to 2–Dimensional QSAR of the same molecule, descriptor computation, variable selection, and statistical approaches are used.

 

Quantitative Structural-Activity Relationship Techniques			2-Dimensional QSAR specification
	Two Set	Assigned Variables/Descriptors	Component/Coefficient	Constant	Analytical statistics
Multiple regressions- Forward Techniques	Training-Set dimensions Size = 63, Test-Set dimensions = 10	Quadrupol-2, MomInertia-X, Zcomp-Dipole, QMDipole -Y	0.018 (± 0.02), -0.010 (± 0.01), 0.0277 (± 0.018), 0.0752 (± 0.031)	0.85	n = 63, Degree of freedom = 14, F-test = 68.19, r2 se =0.02, q2 se = 0.04, pred_r2 =-3.48, pred_r2se =0.30,  r2 = 0.96, q2 =0.92,
Principle Component Regression- Forward Techniques	Training-Sets dimensions Size= 63, Test-Sets dimensions = 10	Quadrupol-2, Zcomp-Dipole	0.005, -0.112, 0.022	1.641	Optimum Components = 4, n = 63 Degree of freedom = 15, F-test = 21.47, r2 se = 0.069, q2 s = 0.100, pred_r2 = -1.14, pred_r2se=0.215, r2 = 0.758, q2 = 0.616
Quantitative Structural -Activity Relationship Techniques	3- Dimensional QSAR specification
	Two Set	Assigned Variables/Descriptors	Component/Coefficient	Constant	Analytical statistics
Multiple Regression- GS 1a – Gs 1k	Training-Sets dimensions Size = 63, Test-Set dimensions = 10	E_78 E_289 E_141	-0.110 (±0.08) 0.052 (±0.062) 0.024 (±0.069)	1.767	n = 63, Degree of freedom = 10, F-test = 2.52, r2 se =0.28, q2 se = 1.12 pred_r2= 0.72, pred_r2se = 0.13, r2 = 0.64, q2 = 0.26
Model i)	Balance Equation I Log-MIC =-0.110 (±0.08 )E_78 + 0.052 (±0.062)E_289+0.024 (±0.069)E_141 + 1.76
Multiple Regression- GS 2ia to GS 4c	Training-Sets dimensions Size = 63, Test-Set dimensions = 10	S_49 E_27 H_6	5.869 (± 1.72) -0.134 (± 0.019) -2.167 (± 0.34)	0.14	n = 63, Degree of freedom = 12, F-test =5.14, r2 se =0.17, q2 se =0.12 pred_r2 =-8.29, pred_r2se = 0.14, r2 = 0.69, q2 =0.11,
Model ii)	Balance Equation II Log-MIC = 5.869 (± 1.72)  S_-0.134 (± 0.019) E_27–2.167 (± 0.34) H_6 + 0.14
Multiple Regression GS 5ia to GS 7id	Training-Sets dimensions Size = 63, Test-Set dimensions = 10	H_19 H_33 S_14	2.12 (± 0.19) 0.54 (± 0.24) -4.01 (± 0.56)	6.2	n = 63, Degree of freedom =11, F-test = 8.05, r2 se = 0.04, q2 se = 0.06 pred_r2 = -74.62, pred_r2se = 0.23, r2 = 0.85, q2 = 0.54,
Model iii)	Balance Equation III Log-MIC = 2.12 (± 0.19) H_19 0.54 (± 0.24) H_33–4.01 (± 0.56) S_142 + 6.2
Multiple Regression GS 8ia to GS 8im	Training-Sets dimensions Size = 63, Test-Set dimensions = 10	H_39 S_12 H_18	5.91 (± 0.03) 164.37 (± 37.01) -6.17 (± 0.03)	10.55	n = 63, Degree of freedom = 12, F-test = 11.38, r2 se = 0.03, q2 se = 0.07 pred_r2 = -0.11, pred_r2se = 0.063, r2 = 0.87, q2 = 0.65,
Model iv)	Balance Equation IV Log-MIC = 5.92 (± 0.04) H_39 +154.37 (± 37.02) S_12 + -6.16 (± 0.03) H_18 + 10.55
Multiple Regression GS 9ia to GS 9ia	Training-Sets dimensions Size = 63, Test-Set dimensions = 10	H_30 S_11 S_31	-0.502 (± 0.001) -7.15 (± 1.53) -7.32 ( ± 0.12)	-3.74	n = 63, Degree of freedom = 12, F-test =217.1, r2 se =0.008, q2 se =0.02 pred_r2 =-12.2, pred_r2se = 0.146, r2 =0.99, q2 = 0.96,
Mode v)	Balance Equation V Log-MIC = -0.502 (± 0.001) H_30+-7.15 (± 1.53)S_11–7.32 ( ± 0.12) S_34-3.74
Principle Component Regression- Forward Techniques	Training-Sets dimensions Size = 63, Test-Set dimensions = 10	E_94, S_74, S_112, E_52	-0.106, 3.517, -0.119, 0.117	0.72	Optimum Components = 4, n = 63, Degree of freedom = 11, F-test = 0.45, r2 se =0.03, q2 se = 0.1 5, pred_r2 =-2.64, pred_r2se =0.27, r2 =0.95, q2 =0.90,
Model vi)	Balance Equation VI Log-MIC = -0.106E_94 +3.517S_74 -0.119 S_112 + 0.117 E_52 +0.72
Partial Least Square Regression-Forward Techniques	Training-Sets dimensions Size = 63, Test-Sets dimensions = 10	E_94, S_74, S_11, E_53	-0.08, 3.61, -0.22, 0.13	0.74	Optimum Components = 4 n = 63 Degree of freedom = 11, F test =115.29, r2se= 0.010, q2 se = 0.04 pred_r2 =-2.21, pred_r2se = 0.28, r2=0.96, q2 =0.92,
Model vii)	Balance Equation VII Log-MIC = -0.08 E_94 + 3.61 S_74 -0.22, S_112 + 0.13 E_53 + 0.74

Table N-. 2 : Equations and QSAR techniques for 2-Dimensional and 3- Dimensional

 

Result and Discussion:

Utilizing the programme V-life MDS -4.6, derivatives of thiazole and oxadiazole chemicals were taken into account for the construction of QSAR models. For an efficient QSAR computation, these datasets are split into training and test-sets. We made sure that molecules in the training and test-sets dimensions were evenly distributed in terms of physical and chemical environment and activity while choosing the training and test sets. The remaining factors were chosen as independent variables, while pharmacological activity was chosen as the dependent variable. For this class of chemicals, the training and test set dimensions of derivatives were chosen at random, and the models/equations were then verified through both intrinsic and extrinsic processes. For discussion, a few QSAR simulations of statistical significance were selected.

Multiple linear regression models in 2-Dimensional QSAR with forward stepwise demonstrate a strong correlation among pharmacological activity and variables. The coefficients of determination QMDipole-Y, MomInertia-X, Quadrupole-2, Zcomp-Dipole and with r2 values of 0.96 and 0.75, being order to articulate 76 percent of the variation in the reported activity indices. Each descriptor made a valuable contribution to the model’s creation. The model’s accuracy is shown by the poor threshold deviation of r2se =0.07, r2­­­­­ se =0.03. The model was internally validated using the end-up leaving method.

            Cross-validated r2 values of 68 percent for the model’s intrinsic predictive ability (q2 = 0.92, q2 = 0.61) indicate that it has a strong intrinsic predictive ability.    Additionally, a 99.5 percent reliability in the created model’s nonrandomness was demonstrated by the randomization test, which led to its selection as the QSAR model. The total empirical probability value of the model is 99.5 percent, as indicated by the F-test=78.19, 20.37, which also indicates that the model’s failure probability is 01.0 in 10,000. The variables reveal an interrelationship between variables used for the resulting QSAR model that is progressive. The favorable coefficients imply adding these atoms of carbon to molecules results in an increase in antiplatelet action.

The first matrix of the quadrupole moments’ magnitude is indicated by the quadrupole-2 descriptor. Its significant QSAR model contribution indicates that it will boost potency. Its significant value implies that increasing the quantity of these atoms would improve antiplatelet activity. These atoms enhance the dipole moment., ZcompDipole,  MomInertiaX, and QMDipoleY descriptors are examples of a form of dipole-dipole interactions, and their contributions to the platelet aggregation-inhibition actions show that the excellent group has strong antioxidant potential.

Figure 6 illustrates the 3-Dimensional perspective of aligned analogues and the contribution of GS 1a – GS 1k descriptors.

 

Figure 7 illustrates the 3-Dimensional perspective of an aligned analogues and the contribution of GS 2ia to GS 4c descriptors

 

Figure 8 illustrates 3-Dimensional perspective of an aligned analogues and the contribution of GS 5ia to GS 7id descriptors

 

 

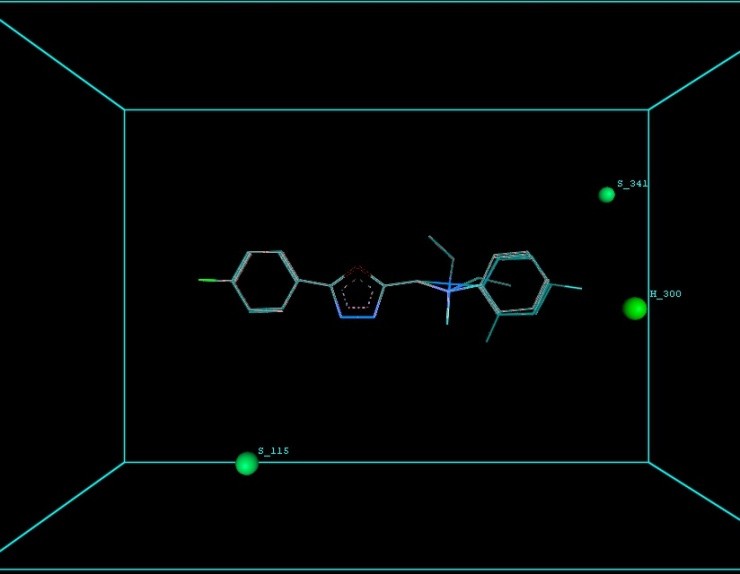
Figure 9 illustrates 3-Dimensional perspective of an aligned analogues and the contribution of GS 8ia to GS 8im descriptors

 

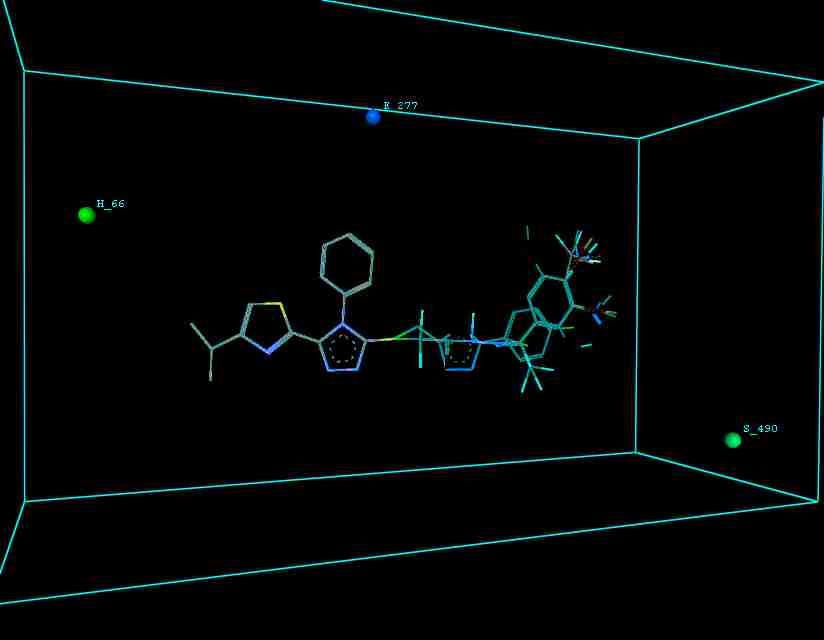
Figure 10 illustrates 3-Dimensional perspective of an aligned analogues and the contribution of GS 9ia to GS 9iI descriptors

Multiple linear regressions with forwarding stepwise and the generated equations in 3-Dimensional QSAR demonstrate the strong correlation between biological activity and variables. With r2 = 0.95, r2= 0.64, r2= 0.85, r2= 0.69, r2= 0.87, r2= 0.99, and r2=0.96, which really is adequate to explain variance in the reported activity indices. The value of q2, which measures a model’s intrinsic predictive capability, and pred r2, which evaluates a model’s potential to forecast the behavior of an external test set, serve as the criteria for selecting a model. Our model appears to be accurate and dependable, according to the cross-validated regression analysis (q2), which was regarded as a gauge of prediction dependability.

The suggested A chance of less than 00.001 exists for the Prediction model. produced by chance, according to the randomization tests. Steric variables and electrostatic variables that contribute to models include E 289, E-141, S-4, H-19, H-33, H-12, H-18, S-11, S-34, S-91, E-94, S-14,  S-5, , E-71, H-30, E-277, S-74, S-11, H-6, E-52, E-9  E-78, The models’ indicative power is represented by the q2 values (q2= 0.96, q2= 0.92, q2= 0.54, q2= 0.24, q2= 0.65, q2 = 0.92, q2= 0.90, q2= 0.11, q2= 0.61).

The derived QSAR equation is statistically significant, as shown by the values of F test, r2 se, q2 se, pred r2, and pred r2se, r2, q2, and it demonstrates that the model’s predictive capacity is 75% (Intrinsic validation) and 70%. (Extrinsic validation). Smaller bulky residues are selected in that location because steric potential there’s really advantageous for activity, according to steric descriptors. In a 3-Dimensional image, the field energies of the steric and electrostatic interactions among the probe (methyl) and the compounds are shown. Steric and electrostatic force contributions show that both forces are more significant than the other.

The preferable substitution (a larger or smaller bulkier group) to create increased antioxidant potential is implied by the steric effect, which occurs when the phenyl ring is in the o- or m- position. The electro+ve (Electron withdrawing) groups is favored at the four positions of the Ph-ring, which is supported by an electrostatic description with a significant positive impact surrounding that location.

 

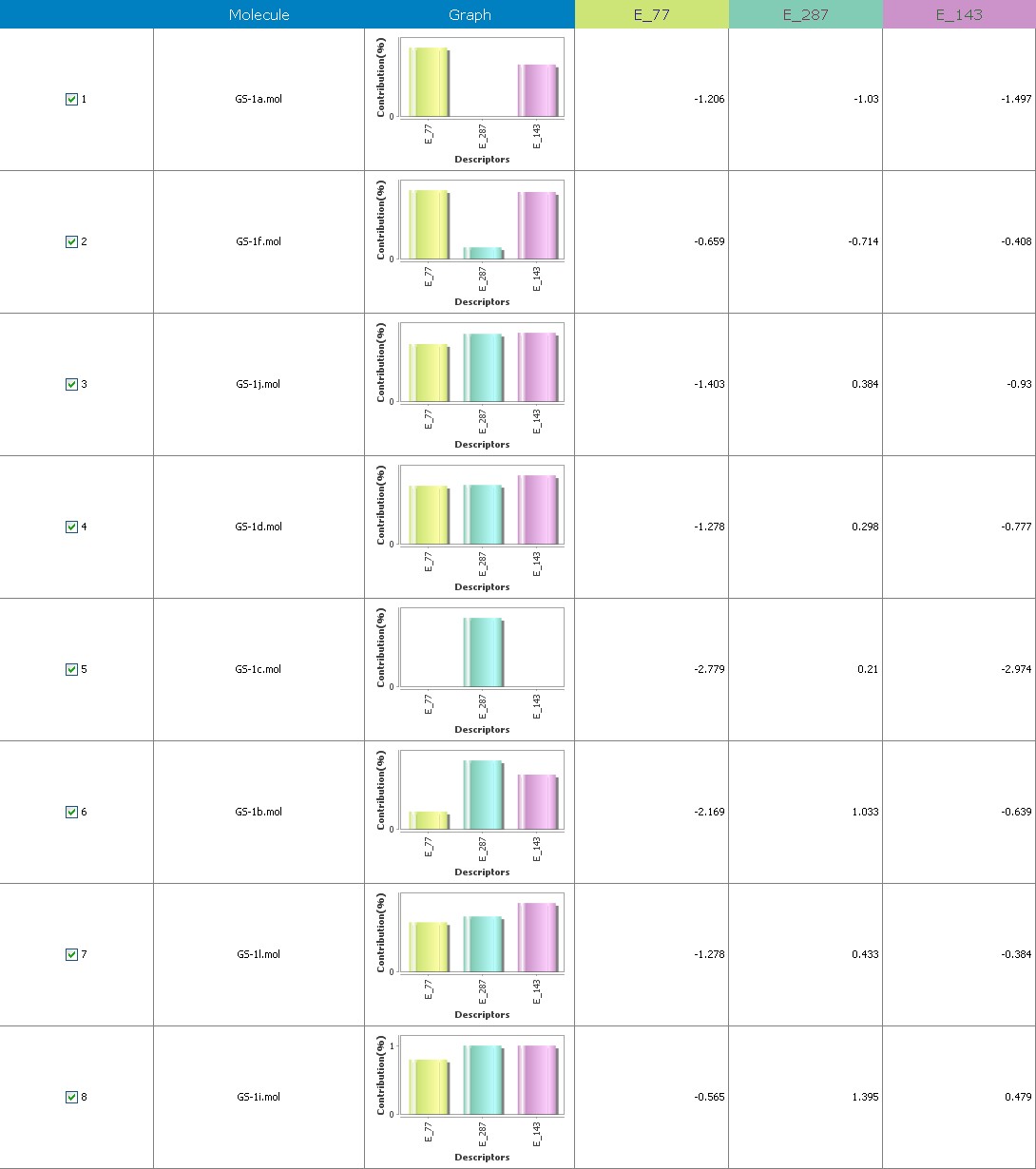
Fig.11 Descriptor participation graphs: GS 1a to GS 1k

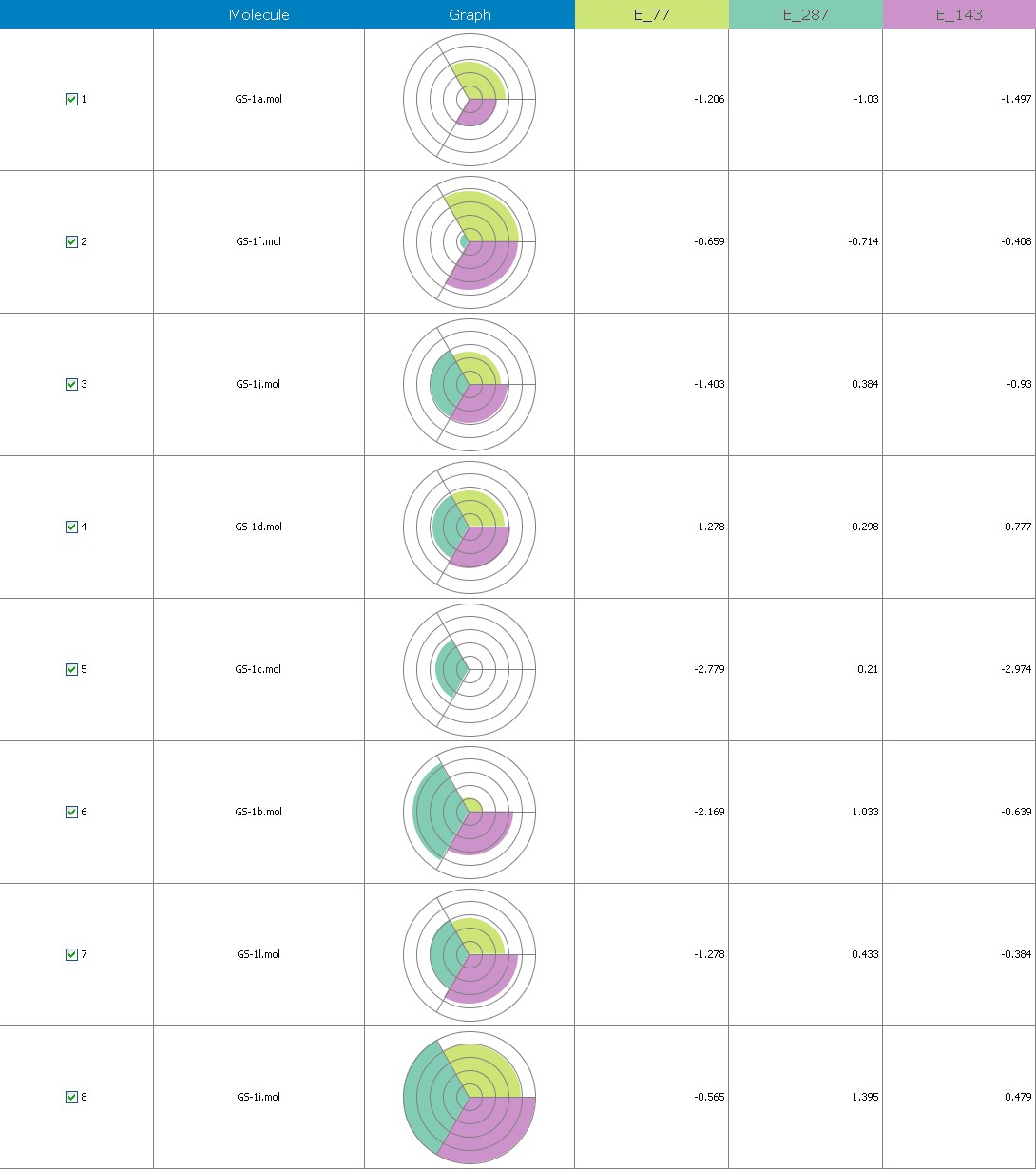
Fig.12 Descriptor participation Pi- graphs: GS 1a to GS 1k

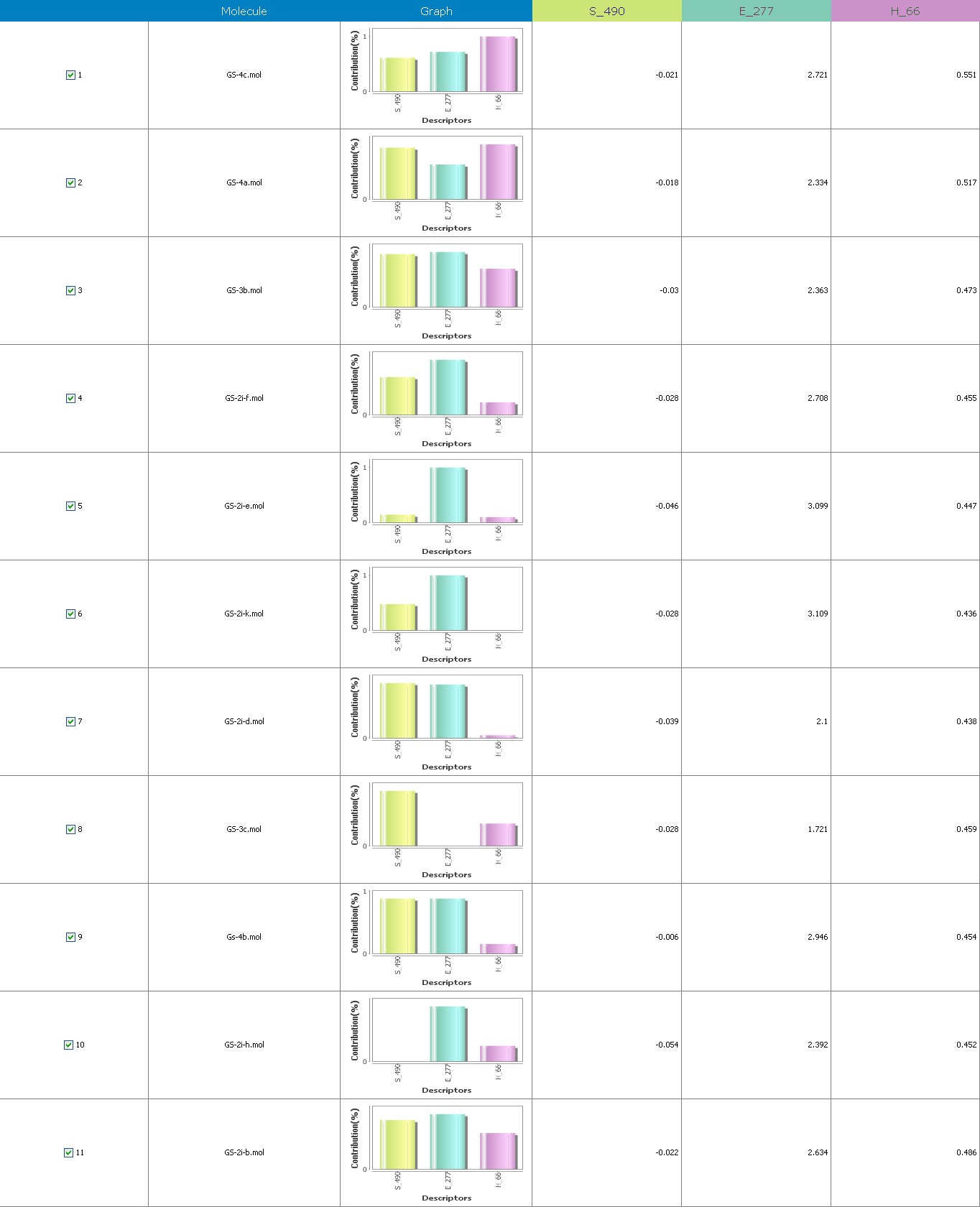
Fig.13 Descriptor participation graphs : GS 2ia to GS 4c

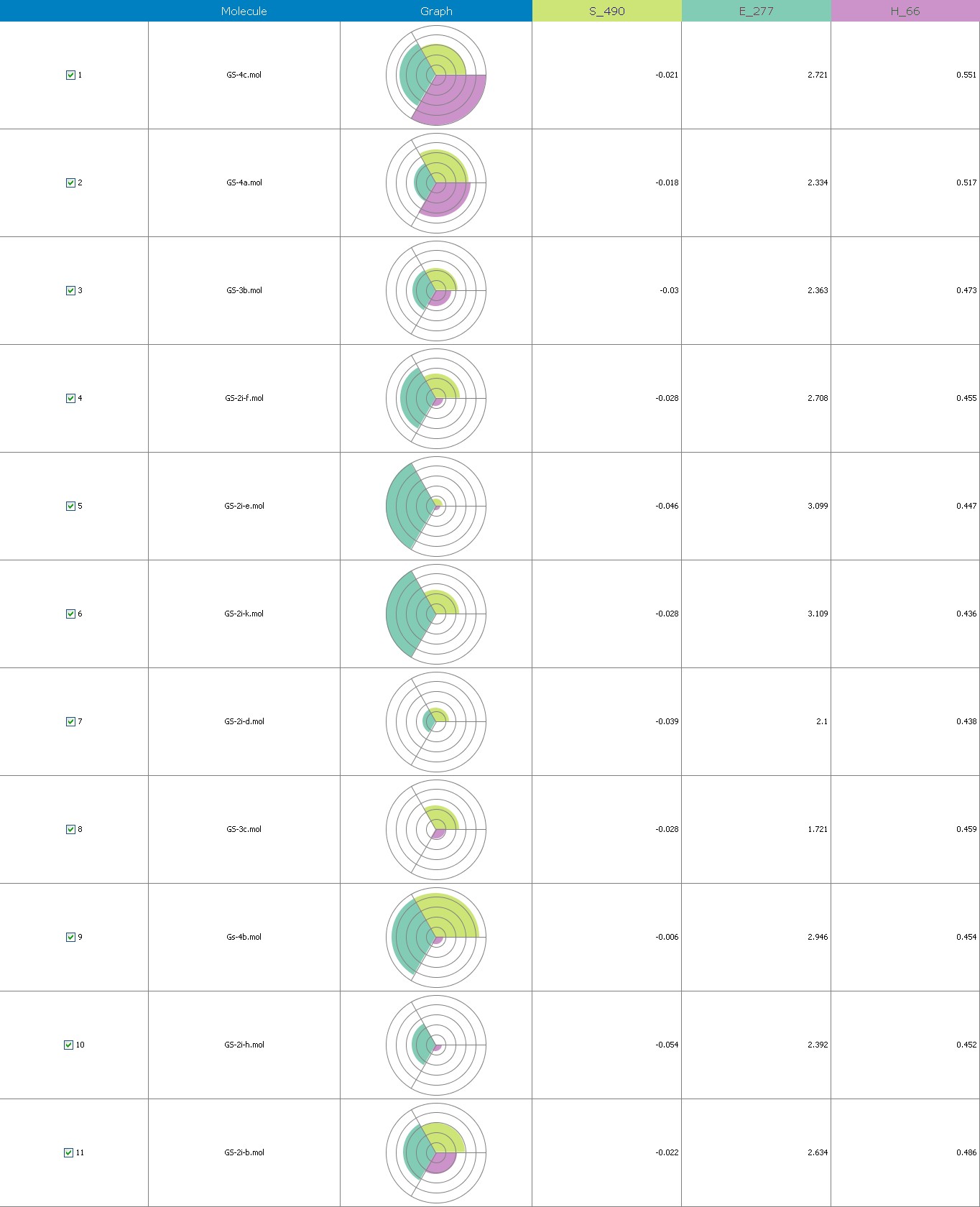
Fig.14 Descriptor participation Pi-graphs: GS 2ia to GS 4c

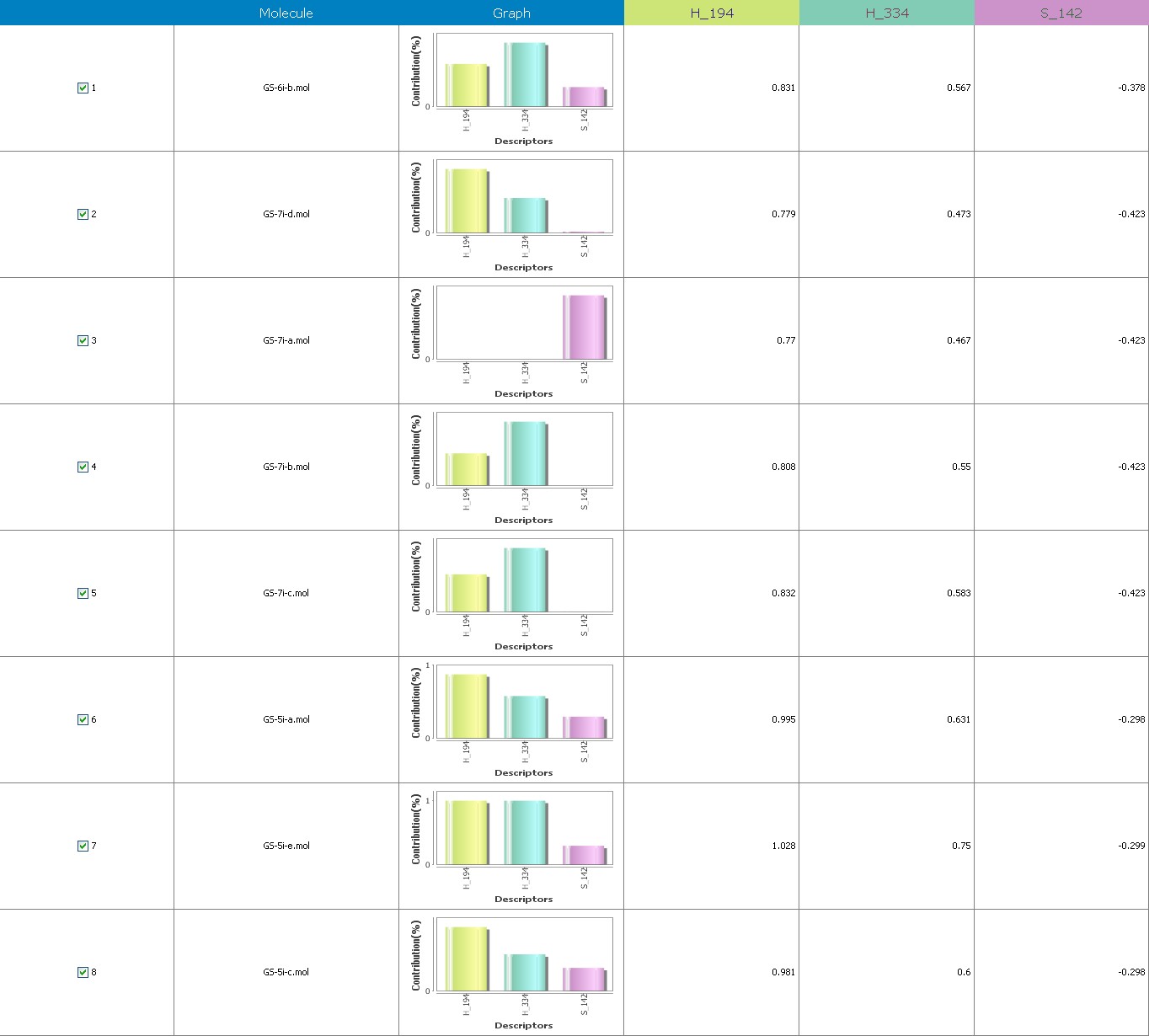
Fig.15 Descriptor participation graphs : GS 5ia to GS 7id

 

 

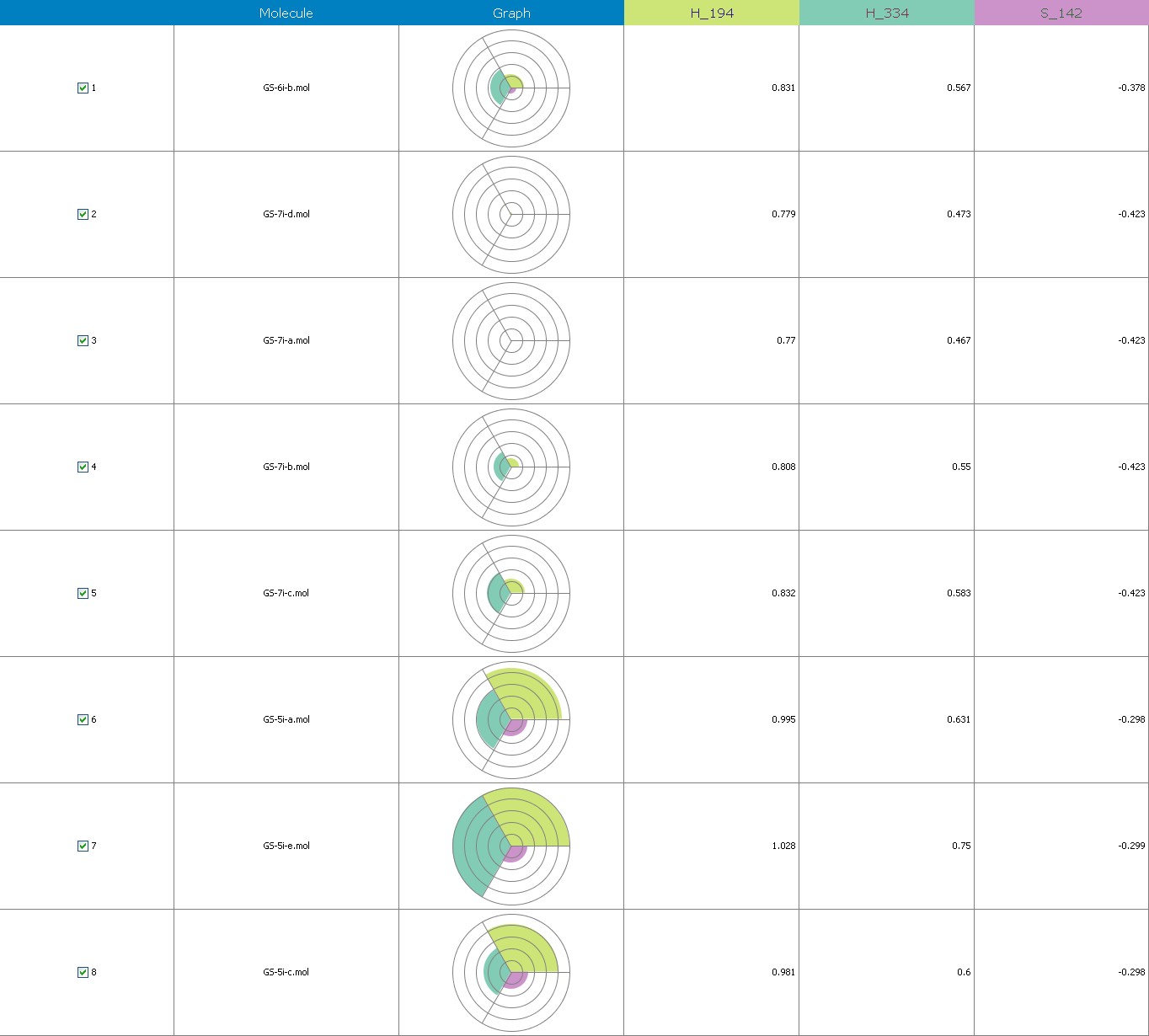
Fig.16 Descriptor participation Pi-graphs: GS 5ia to GS 7id

 

 

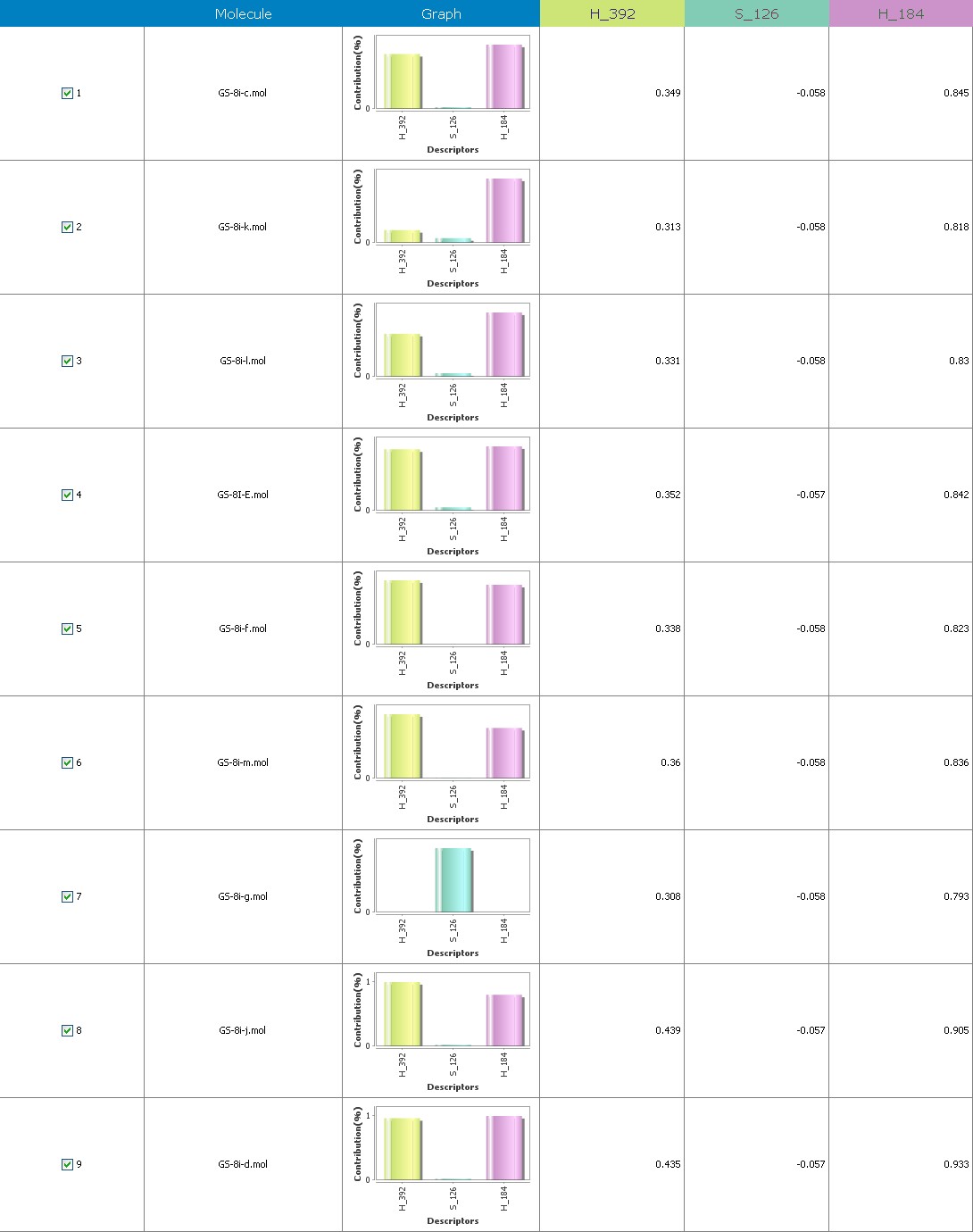
Fig.17 Descriptor participation graphs: GS 8ia to GS 8im

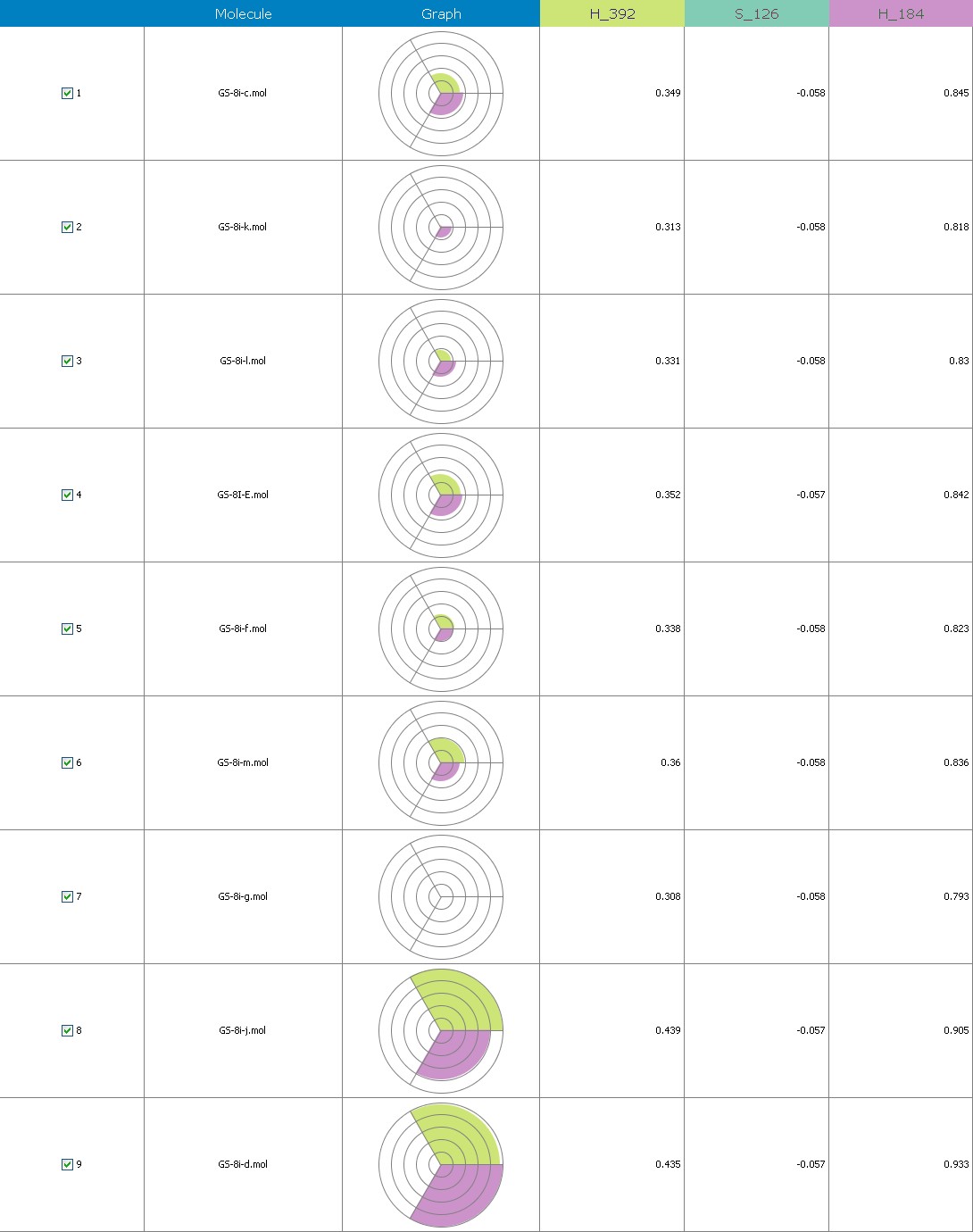
Fig.18 Descriptor participation Pi-graphs: GS 8ia to GS 8im

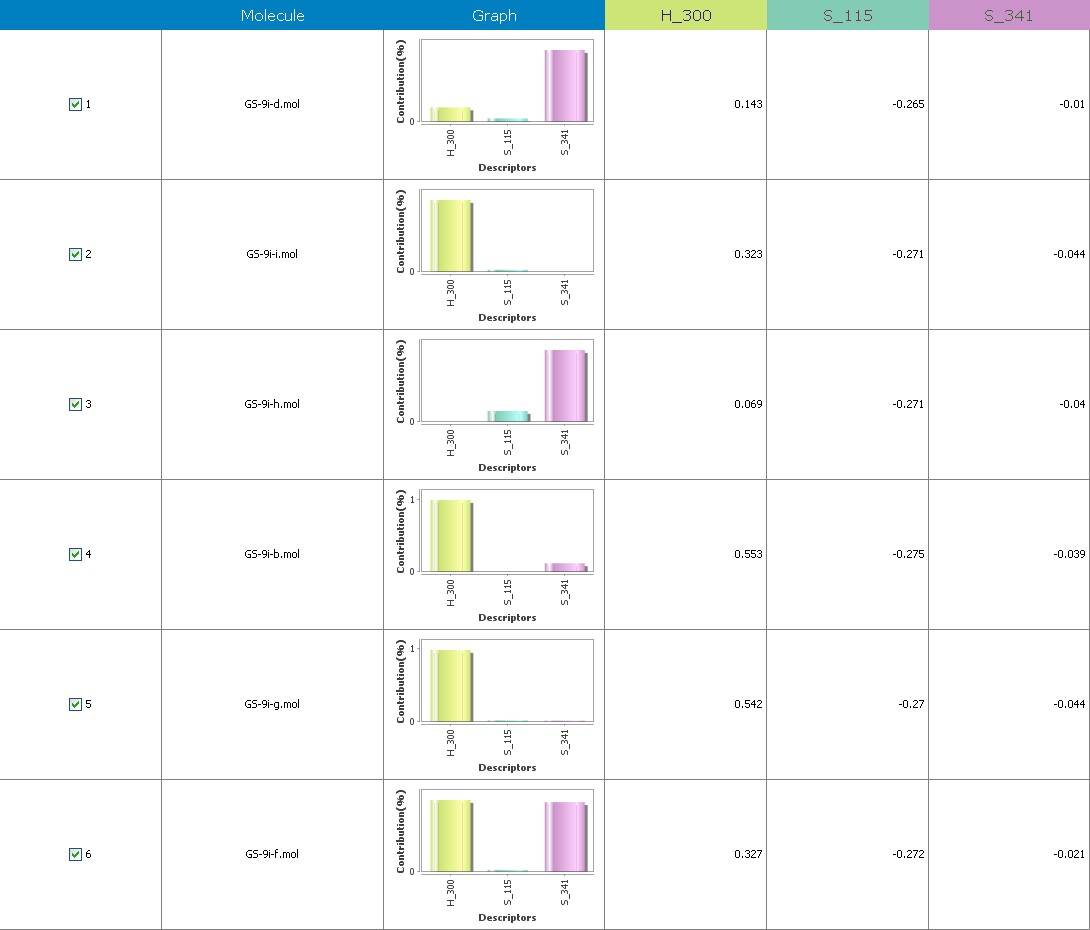
Fig.19 Descriptor participation graphs: GS 9ia to GS 9ii

 

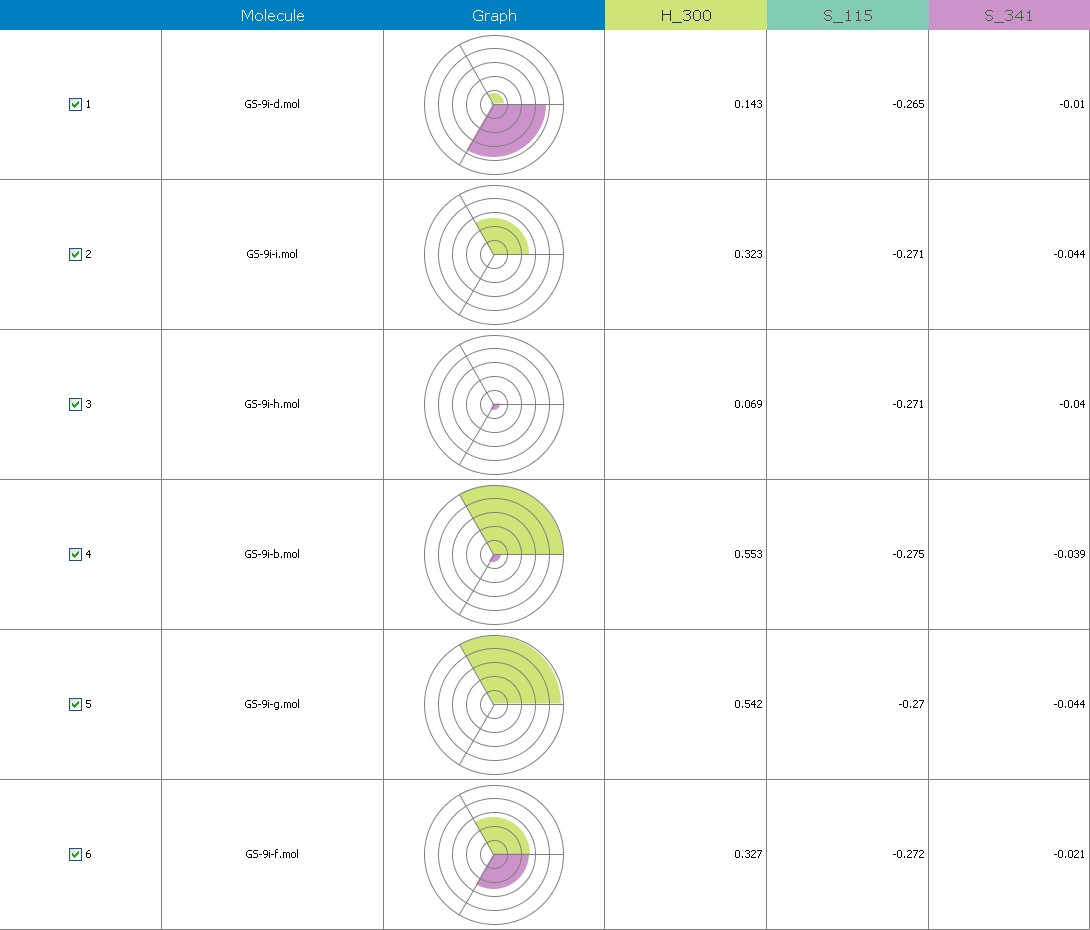
Fig.20 Descriptor participation Pi-graphs: GS 9i a to GS 9ii

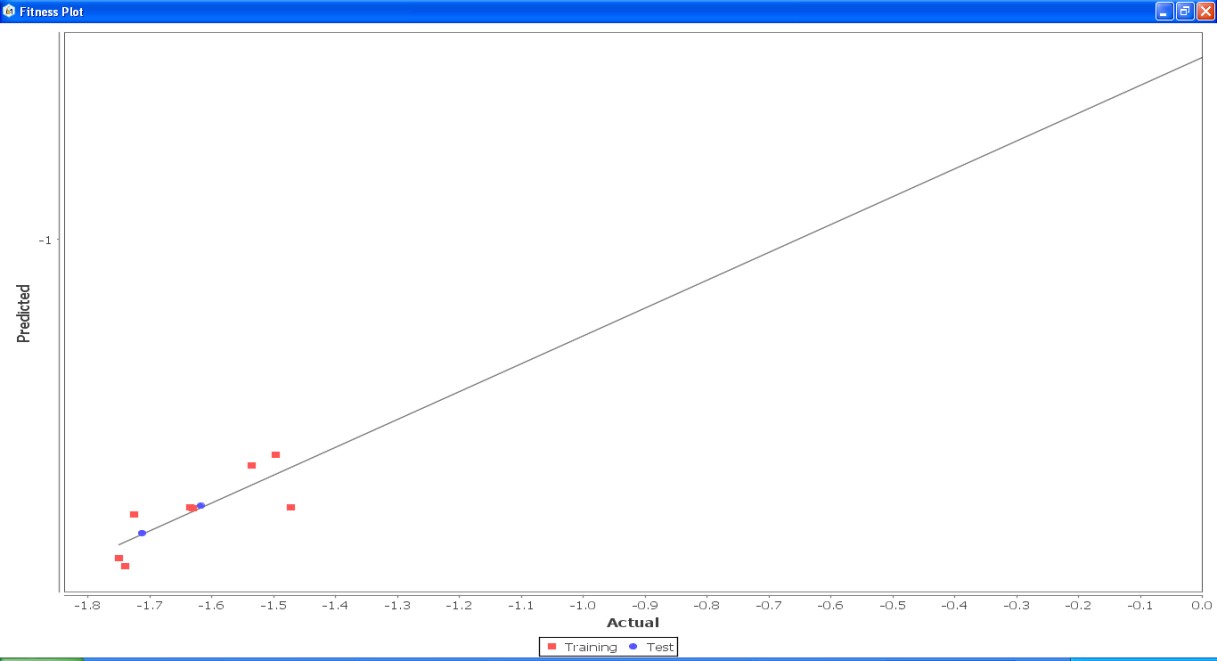
Fig. 21: Fitness graph comparing GS 1a – GS 1k between reported activity and expected activity

 

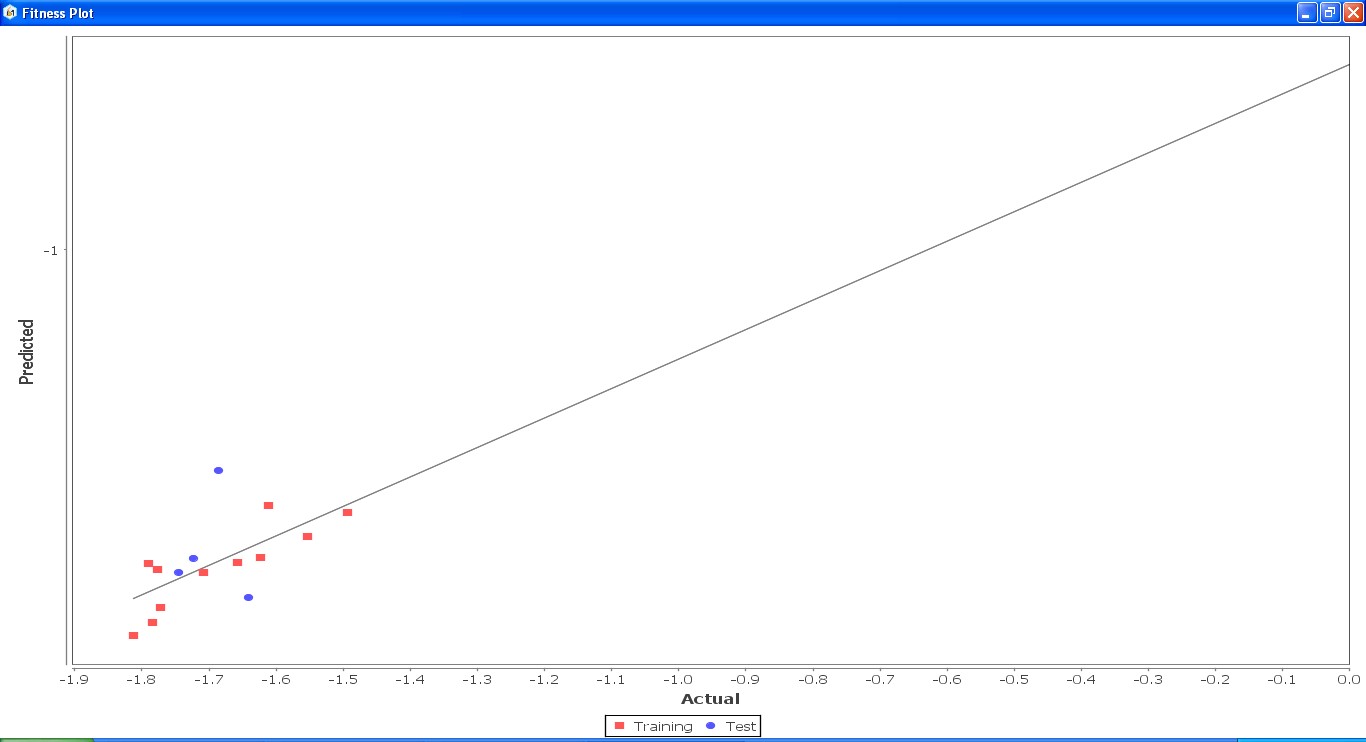
Fig. 22: Fitness graph comparing GS 2ia – GS 4c between reported activity and expected activity

 

 

 

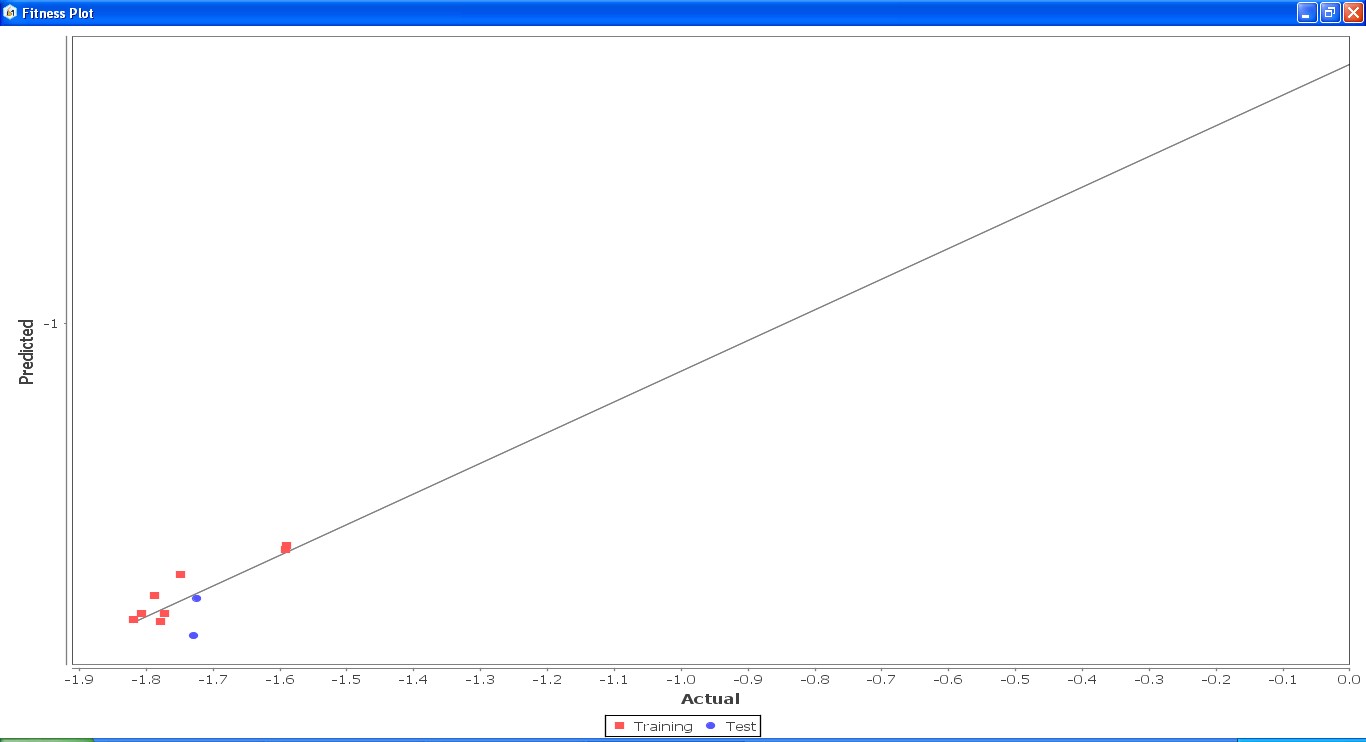
Fig. 23: Fitness graph comparing GS 5ia to GS 7id between reported activity and expected activity

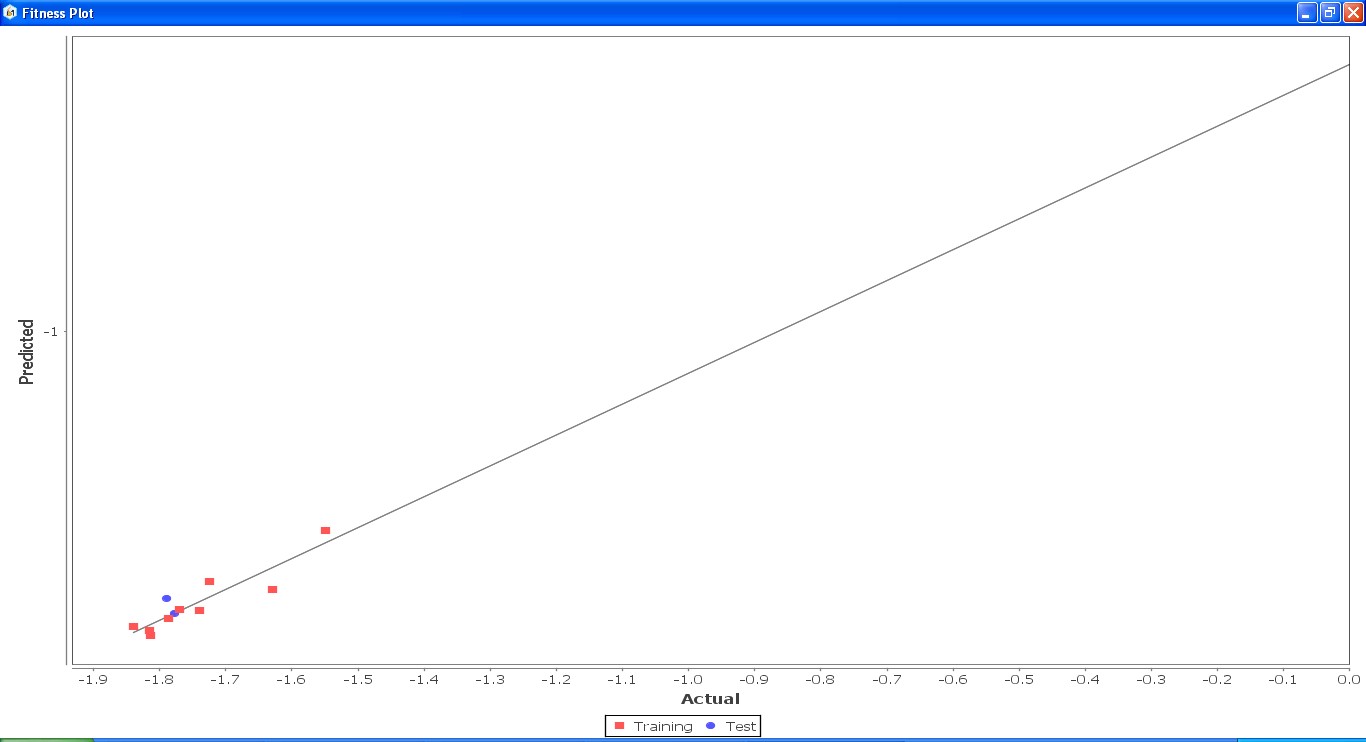
Fig. 24: Fitness graph comparing GS 8ia to GS 8im between reported activity and expected activity

Fig. 25: Fitness graph comparing GS 9ia to GS 9iI between reported activity and expected activity

 

 

Conclusions

Equation-1 has an intrinsic predictive ability of 92 percent (q2) and an extrinsic predictive ability of 32 percent (pred r2se) and explains 98 percent (r2 = 0.64) of the training set’s dimensions total variance. The training set’s dimensions total variance is explained by the equation- 2 in 96 percent of cases (r2 = 0.69), and it also possesses intrinsic (q2) and extrinsic (pred r2se) predictive abilities of 92and 26 percent, respectively.

Equation-3 has intrinsic (q2) and extrinsic (pred-r2se) prediction abilities of 94% and 29%, respt., and demonstrate 97% (r2= 0.87) of the entirety variation in the training-set dimensions. By using the forward method, the descriptor extent is H-66, H-19, H-33, H-39, H-18, H-30, H-29 (0.44 to 0.45), which signifies that a smaller bulky substituent group is preferred in that area. +Ve hydrophobic descriptor range suggests that +Ve water-insoluble potential is favorable for extension in the antiplatelet activity.

The development of 2-Dimensional and 3-Dimensional QSAR models and equations with moderate-to-high thiazole derivatives prediction accuracy. Hydrophobicity’s significance as a 3-Dimensional feature was established, and it was discovered that electrostatic and steric impacts also support antioxidant action. The acquired models could aid in the development of novel active thiazoles with antioxidant properties.

 

Acknowledgments

The “Suresh Gyan Vihar University,” which provided the V-Life MDS software and more, is heartily appreciated by the writers. The principal of the institute is thanked by the authors for providing the resources needed to complete the study. The authors also acknowledge the researchers would like to thank whose insightful criticism and recommendations considerably enhanced the work.

REFERENCES

1. Ajmani S, Jadhav K and Kulkarni SA. Three-dimensional QSAR using the k-nearest neighbor method and its interpretation. Journal of Chemical Information & Modeling 2006;46:24–31.
2. Bhadoriya KS, Jain SV, Bari SB, Chavhan ML and Vispute KR. 3D-QSAR study of indol-2-yl ethanones derivatives as novel indoleamine 2, 3-dioxygenase (IDO) inhibitors. European Journal of Chemistry 2012;9:1753–59.
3. Ivanka M. Tsakovska QSAR and 3D-QSAR of Phenothiazine Type Multidrug Resistance Modulators in P388/ADR Cells. Bioorganic & Medicinal Chemistry 2003;11:2889–99.
4. Clark M, Cramer III RD, and Van ON, Validation of the general-purpose Tripose 5.2 force field. Journal of Computational Chemistry 1989;10:982– 1012.
5. Cramer III RD, Patterson DE, and Bunce JD. Comparative molecular field analysis (CoMFA) 1. Effect of shape on binding of steroids to carrier proteins. Journal of American Chemical Society 1988;110:5959–67.
6. Akira M, Masakazu S, Mari A, Makoto T. 2-Acylimino-3H-thiazoline Derivatives: A Novel Template for Platelet GPIIb/IIIa Receptor Antagonists. Bioorganic & Medicinal Chemistry Letters 2001;11:1031–35.
7. Doweyko AM. QSAR: dead or alive? J Comput Aided Mol Des 2008;22:81–89.
8. Yadav JS, Subba Reddy BV, Gopala Rao Y, Narsaiah AV. The first example of the coupling of a-diazo ketones with thiourea: a novel route for the synthesis of 2-aminothiazoles. Tetrahedron Letters 2008;49:2381–83.
9. Gaurav A, Yadav MR, Giridhar R, Gautam V and Singh R. 3D-QSAR studies of 4-quinolone derivatives as high-affinity ligands at the benzodiazepine site of brain GABAA receptors. Medicinal Chemistry Res 2010; Available from URL: http://dx.doi.org/10.1007/s00044-010-9306-5.
10. Ghosh P and Bagchi MC. QSAR modeling for quinoxaline derivatives using genetic algorithm and simulated annealing-based feature selection. Current Medicinal Chemistry 2009;16:4032–48.
11. Halgren TA. Merck molecular force field: III. Molecular geometries and vibrational frequencies for MMFF94. Journal of Computational Chemistry 1996;17:553–86
12. Hansch C. A quantitative approach to biochemical structure activity relationships. Account of Chemical Research 1969;2:232–39.
13. Jain SV, Bhadoriya KS, and Bari SB. QSAR and flexible docking studies of some aldose reductase inhibitors obtained from natural origin. Medicinal Chemistry Research 2012;21:1665–76. Available from: URL: http://dx.doi.org/ 10.1007/s00044-011-9681-6.
14. Jain SV, Ghate M, Bhadoriya KS, Bari SB, Chaudhari A, and Borse JS. 2D, 3D-QSAR and docking studies of 1,2,3-thiadiazole thioacetanilides analogues as potent HIV-1 non-nucleoside reverse transcriptase inhibitors. Organic Medicinal Chemistry Letters 2012;2:22. Available from: URL:http://dx.doi.org/10.1186/2191-2858-2-22.
15. Nakka S and Guruprasad L. The imidazolidone analogs as phospholipase D1 inhibitors: analysis of the three-dimensional quantitative structure–activity relationship. Medicinal Chemistry Research 2012;21:2517–25. Available from: URL:http://dx.doi.org/10.1007/s00044-011-9773-3.
16. Radhika V, Kanth SS and Vijjulatha M. CoMFA and CoMSIA studies on inhibitors of HIV-1 integrase-bicyclic pyrimidinones. Journal of Chemistry. 2010; 7(S1):S75–S84.
17. Sahu NK, Bari SB and Kohli DV. Molecular modeling studies of some substituted chalcone derivatives as cysteine protease inhibitors. Medicinal Chemistry Research 2011; Available from URL: http://dx.doi.org/10.1007/s00044-011-9900-1.
18. Scior T, Medina-Franco JLDoQT, Martinez-Mayorga K, Yunes Rojas JA, Bernard P. How to recognize and workaround pitfalls in QSAR studies: a critical review. Current Medicinal Chemistry 2009;16:4297–13.
19. Sharma MC and Kohli DV. A comprehensive structure-activity analysis 2,3,5-trisubstituted 4,5-dihydro-4-oxo-3H-imidazo [4,5-c] pyridine derivatives as angiotensin II receptor antagonists: using 2D- and 3D-QSAR approach. Medicinal Chemistry Research 2012 Available from URL:http://dx.doi.org/10.1007/s00044-012-0040-z.
20. Shen M, Xiao Y, Golbraikh A, Gombar VK and Tropsha A. An in silico screen for human S9 metabolic turnover using KN nearest neighbor QSPR method. Journal of Medicinal Chemistry 2003;46:3013–20.
21. Tanneeru K, Reddy BM and Guruprasad L. Three-dimensional quantitative structure–activity relationship (3D-QSAR) analysis and molecular docking of ATP-competitive triazine analogs of human mTOR inhibitors. Med. Chem. Res. 2011; Available from: URL: http://dx.doi.org/10.1007/s00044-011-9629-x.
22. VLife MDS 3.5, Molecular Design Suite. Vlife Sciences Technologies Pvt. Ltd. Pune. 2010.
23. Zheng W and Tropsha A. Novel variable selection quantitative structure-property relationship approach based on the k-nearest neighbor principle. Journal of Chemistry Information and Computer Science 2000;40:185–94.
24. Mukesh CS, Kohli DV. Insight into the structural requirement of aryltriazolinone derivatives as angiotensin II AT1 receptor: 2D and 3D-QSAR k-Nearest Neighbor Molecular Field Analysis approach. Medicinal Chemistry Research 2012;21(10):2837-53.
25. Verma J, Khedkar VM. 3D-QSAR in drug design–a review. Current topics in medicinal chemistry 2009;10(1):95-115.