1KamleshLakhwani, 2Manish Kumar Sharma, 3Pooja Agarwal
1Vivekananda Institute of Technology
2Poornima College of Engineering
3Poornima College of Engineering
Abstract—Inthis paper, a new optimization method is proposed based on the combination of Ant Colony Optimization and Chaos Theory to solve Dynamic Travelling Salesman Problem. Ant Colony Optimization algorithm has been adapted in a way by using chaos theory to obtain an optimal solution to solve DTSP. By use of both chaos theory and Ant Colony Optimization algorithm, a hybrid algorithm is produced which presented a better net to solve DTSP. In hybrid algorithm, pheromone informing rule is performed by using Logistic Map function and is non-linear which can prevent untimely convergence. Features such as high correctness and good convergence rate to reach best results show our proposed hybrid algorithm is better.
Key words: Dynamic travelling salesman problem, Ant Colony Optimization, Chaos theory, Genetic algorithm, Hybrid Algorithm
I. INTRODUCTION
The Travelling Salesman Problem (TSP) is a standard problem of combinatorial optimization of procedures research area. The objective is to find a shortest visit through a given no. of locations such that every site is visited exactly once. There are several convenient uses for this problem, such as vehicle routing with the additional limitations of vehicle’s path, such as power of vehicles , drilling problems, minimize waste , clustering data arrays , X-ray crystallography, shot sequence generation for scan lithography and many others. This difficulty has also been used during the last years as comparison basis for improving several optimizations methods, such as genetic algorithms, simulated annealing, tabu search, local search, ant colony and Branch and Bound (B&B). The major types of B&B used to solve the TSP are: The best recognizedcorrect algorithms are based on either the B&B technique for the Asymmetric TSP (ATSP) or the Branch or Cut method for the Symmetric TSP (STSP) using the double index formulation of the crisis. Currently, we ignore high cost arcs for the TSP. A disadvantage of this policy is that expenses of arcs and edges are not accurate signs whether those arcs or edges are keeps in an optimal TSP result.
State-of-the-art B&B algorithms for the ATSP can be found and later. The algorithms by Miller and Carpanetorelate patching to find upper bounds, use AP lower bounds, and branch on a smallest cycle in the current AP solution, i.e., a cycle of minimum cardinality. On the other hand, a list of sub problems should be preserved in order to decide the most promising one. As a consequence, BFS algorithms are inclined to run out of memory when the search trees develop large. Upper bounds of Branch & bound algorithm for the ATSP was enhanced by with iterative patching which is a process for build good possible solutions of the ATSP. Iterative patching events reduce the number of sub problems in the spanning B&B tree, so that minor computation times are needed. This technique only considers the time intense problems. In this paper, while maintaining that our algorithm is earlier than that of Branch and Bound for most of the problems, new computational results which are obtained after cleansing the arrangement of the alphabet table for the Truncated Time Dependent Travelling Salesman Problem (TTDTSP) is being accessible in this paper. Travelling salesman problem (TSP) is a distinguished, well-liked and broadly studied problem in the field of combinatorial
optimization and attracts computer researchers, mathematicians and others. Its statement is deceivingly simple, but yet it remains one of the most demandingand challenging problems in operational research. It also an optimization difficulty of finding a shortest closed tour that travels all the given cities. It is identified as a classical NP-complete problem, which has very large search spaces and is very hard to solve.
Problem Introduction:The Traveling Salesman Problem (it is also referred to as the TSP) can be represented in a lot of different behavior. The first one initiated below is the unique version and which will be the center of attention of our study of the TSP. The examples following demonstrate other ways to present this problem. We will show different examples about the Traveling Salesman Problem.
II. Procedure for Paper Submission
Chaos theory
Chaos is a kind of universal nonlinear phenomena in all areas of science, which occurs in many systems .It is generally known as its significant dynamic characteristics: periodicity, intrinsic stochastic property and the sensitive dependence on initial conditions. The uncertainty of chaos is a result of the understanding of chaotic systems to the initial situations, so the chaos association could go through every state in convinced scale according to its own reliability and periodicity. It could be introduced into the optimization approach to increase speed the optimum seeking procedure and find the universal optimal result.
The most popular and simplest chaotic meaning is known as logistic mapping purpose which occupies a differential equation of non-linear first order single – variable. The active equation of this function was initially introduced by Robert May. It is defined as follow
Xn+1=(Lambda)XN(1+XN)…………………………………….. (1)
In Equation (1), x value in interval [0, 1] and r value in interval 0<r≤4 are accepted. This function shows three chaotic behaviors in which the Equation (1) behavior is considered as follow if X0=0.3 Pseudo code algorithm of non- linear logistic function is as follow:
- Initialization X
(n) = Fixed Point r= Chaotic Point
- Loop
- (n+1) =r*X (n)* (1-X (n))
- Until Terminated
Fig shows the output in the first 30 iterations for r=2.8 which is almost chaotic. But as passing through transient state, the final response reaches to the non-zero value.
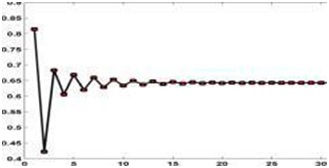
As Figure 1 shows the final answer between two constant numbers will change as r=3.2
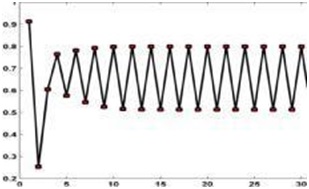
Figure2: Signal Chaotic Behavior for r=3.2
- The Theory of Ant Algorithm
The Ant Colony Optimization methods has materialized recently as a comparatively novel meta-heuristic for hard combinational optimization problems. It is designed to reproduce the capability of ant colonies to conclude shortest paths to food. Although individual ants posses few competences, their operation as a colony is capable of complex performance. Real ants cannot directly communicate by pheromone information without using visual cues and are capable of finding the shortest path between food sources and their nests. The ant deposits pheromone on the trail while walking, and the other ants follow the pheromone trails with some chance which are balanced to the concreteness of the pheromone. The more ants walk on a trail, the more pheromone is deposited on it and more and more ants go after the trail. Through this method, ants will ultimately find the shortest path. Artificial ants reproduce the behaviour of real ants how they search the food, but can solve much more complex problems than real ants can. A search algorithm with such concept is called Ant Colony Optimization.
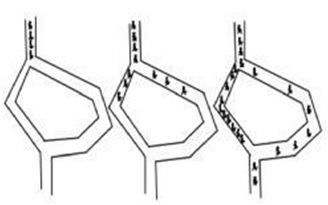
Figure 3: shows how the ants find the shortest path.
(Sketch map of the ant theory)
III. PROPOSED SOLUTION
Chaos contains a series of repetitive activities for algorithms optimization to progress and get faster its performance. Ants chaotic performance make pheromone remains reliable on all manes so that ant can discover the nearer directions in the shorter time. So, we can discover a way of repetitive points, it can be used to optimize direction.
Optimization is demanding to change a primary idea to an optimal response. Practically, optimization issues are so difficult and standard algorithms can’t solve them
satisfactorily. These algorithms have two restrictionsdiminishing in local smallest amount and time overshadowing to search. At one hand, due to dynamic and unplanned features of chaos variables, chaos systems are capable of avoidance from local best possible. So, chaos searching can be used nearly to optimize cooperative intelligence algorithms.
In the proposed algorithm, by using the arrangement of logistic map is one dimensional and ACO about DTSP, it is studied the optimization of the found routes by ants through the chance of selecting directions and updating pheromone to chooses about which routes will be better to choose.
Well Distribution Strategy of Initial Ants
At the beginning of ACO algorithm, some paths are walked through by the ants, others are never passed. The local heuristic controlled by visibility, encourages them to choose cities which are closer. This means that they are likely to decide to travel along short edges. Thus some cities may have many ants while some cities may have no ant at all. Because the amount of pheromone on each path is originallyindistinguishable, therefore the ant mainly uses the detachment between the two cities as the heuristic factor when it chooses the next city. In this way, when there are comparatively more ants in a certain city, the compactness of the pheromone on a convinced path will be strengthened due to the comparatively larger number of ants travelling along the path. The path is not essentially the shortest path that local best solution is searched out or ants arrive at stagnation state. In order to solve this difficulty, the system adopts a process to distribute the ants consistently, i.e., position mantes to n cities and make sure that each city collects at least one ant. Thus, the search space of the explanation is distended and the possibility of getting the optimal result is improved.
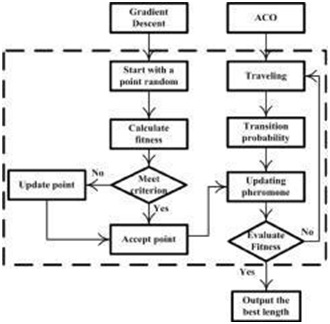
Figure 4:Flowchart of the Proposed Algorithm
Pseudo-code of the proposed algorithm based on ACO algorithm and chaotic function include as below:
- Begin
- Initialization Parameters
- Loop
Each ant is positioned on a starting City
- Loop
Transition probability rule
Pheromone updating
Logistic Function
- Until All ants have built a complete solution
- Until End condition
- End.
IV. RESULTS AND DISCUSSION:
In this section, we evaluate the achieved results from proposed algorithm to solve DTSP. In order to indicate the efficiency of proposed algorithm, we consider 30 cities and maximum 100 iterations for two algorithms. By considering the possibility of route selecting changes and updating method as chaotic, we can review the tour length. In Fig.5, the cities are drawn as dots on the coordinates.
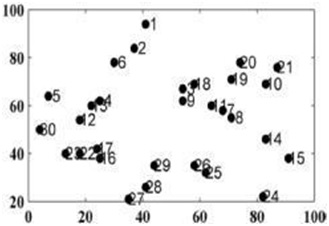
Figure 5: Cities Coordinate
V. CONCLUSION:
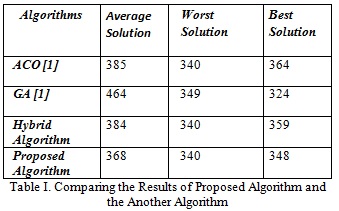
In this paper, we introduce a new method based on ACO and chaos theory to find optimal route. The obtained results in this techniquedesignate the optimal solution and appropriate efficiency of the algorithm in solving DTSP. It also improved significantly the meeting rate and explanation quality in compared with optimization approach based on ants performance. In this paper, we have described a new method for optimizing the DTSP. In problem solving of DTSP meta-innovative methods are used mainly.This paper presents an approach for solving traveling salesman difficulty based on improved ant colony algorithm. The main involvement of this paper is a study of the prevention of stagnation behavior and premature convergence by using distribution policy of initial ants and dynamic heuristic factor updating based on entropy.
Although ACO presents acceptable and correct solutions to explain DTSP, but the proposed algorithm can progress the problem explanations if we use chaos theory and substitute a non-linear logistic function.An enhanced version of ACO algorithm based on candidate list policy and also proposed dynamic heuristic factor updating based on entropy and mergence of local search explanation is proposed. From our experimental results, the planned system is more successful than the ACS algorithm in terms of meeting speed and the ability to discover better solutions.
REFERENCES
- B.Li, W.S.Jiang, “Optimizing complex functions by chaos search,” Cybernetics and Systems: An International Journal, Vol. 29, pp. 409-419, 1998.
- C. Li, M. Yang, L. Kang: “A New Approach to Solving Dynamic Traveling Salesman Problems“. In: Wang, T.-D., Li, X., Chen, S.-H., Wang, X., Abbass, H., Iba, H., Chen, G., Yao, X. (eds.) SEAL 2006. LNCS, Springer, Heidelberg, vol. 4247, pp. 236–243, 2006.
- D. E.Goldberg, “Alleles Loci and the TSP”, Proceedings of the First International Conference on Genetic Algorithms and Their Application, Lawrence Erolaum, New Jersy, pp.154-159, 1985.
- F. S. Gharehchopogh, I. Maleki, M. Farahmandian, “New Approach for Solving Dynamic Traveling Salesman Problem with Hybrid Genetic Algorithms and Ant Colony Optimization”, International Journal of Computer Applications (IJCA), Vol. 53, No.1, pp 39-44, September 2012.
- H. K.Tsai, J. M.Yang, Y.F. Tsai, C.Y. Kao, “Heterogeneous selection genetic algorithms for traveling salesman problems”, Engineering Optimization, Vol. 35, No.3, pp. 297–311, 2003.
- H.N Psaraftis,”Dynamic vehicle routing problems”. In: Golden, B.L., Assad, A.A. (eds.) Vehicle Routing: Methods and Studies, Elsevier, Amsterdam, pp.223–248, 1988.
- J. Pepper, B. Golden, E. Wasil, “Solving the traveling salesman problem with annealing-based heuristics”: a computational study. IEEE Transactions on Systems, Man, and Cybernetics, Part A, Vol. 32, pp. 72 – 77, 2002.
- K. Aihara, T. Takabe, M. Toyoda, “Chaotic neural network”. PhysLett A, Vol. 144, pp.333-40, 1990.
- K. S.Leung, H.D. Jin, Z. B. Xu, ”An expanding self-organizing neural network for the traveling salesman problem”, Neurocomputing, Vol. 62, pp. 267–292, 2004.
- L. Pecora, T. Carroll, “synchronization in chaotic system”. Phys Rev Lett, Vol. 64, pp.821-4, 1990.
- M. Albayrak, N.Allahverdi, “Development a new mutation operator to solve the Traveling Salesman Problem by aid of Genetic Algorithms”, Expert Systems with Applications, vol. 38, no.3, pp. 1313–1320, 2011.
- M. Dorigo, G. Di Caro, and L. M. Gambardella.”Ant algorithms for discrete optimization”.Artificial Life, Vol. 5, No. 2, pp.137–172, 1999.
- M. Dorigo, V. Maniezzo, and A. Colorni, “The ant system: Optimization by a colony of cooperating agents”, IEEE Transactions on System, Man, and Cybernetics, Part B, Vol. 26, pp. 29-41, 1996.
- M. Dorigo and L. M. Gambardella, “The colony system: A cooperative learning approach to the traveling salesman problem”
- M.Dorigo, L. M.Gambardella, “Ant colony system: a cooperative learning approach to the traveling salesman problem”, IEEE Transactions on Evolutionary Computation, Vol. 1, No. 1, pp.53–66, 1997.
