FRACTIONAL DERIVATIVE PERTAINING TO I-FUNCTION AND LAURICELLA FUNCTION

*HARSHITA GARG AND **ASHOK SINGH SHEKHAWAT

*Suresh Gyan Vihar University, Jagatpura, Jaipur, Rajasthan, India

**Arya College Of Engineering And Information Technology, Jaipur, Rajasthan, India

          

 Abstract :

The object of this paper is to obtain a fractional derivative of I- function associated with generalize Lauricella  functions and general   class of multivariable polynomials.

 Key words: Fractional derivative operator, I-function, Lauricella function, general class of   multivariable    polynomials. 

 INTRODUCTION:

The I- function given by Saxena [4] is     represented and defined as following:

 

                                

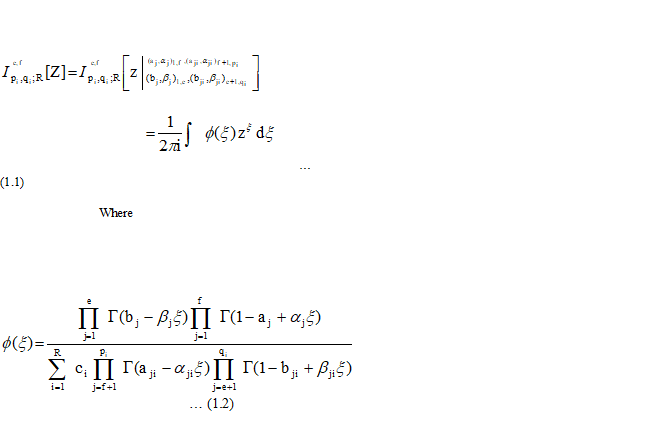
   pi (i= 1,….,R), qi (i= 1,….,R), e, f are integers satisfying 0 £ f £ pi, 0 £ e £ qi (i= 1,….,R); R is finite, αj, βj,  αji, βji,  are real and positive; aj, bj,  aji, bji are complex numbers and £ is the path of integration separating the increasing and decreasing sequences of poles of the integrand.

The integral converges if

                      

                                                                           ,

 

         

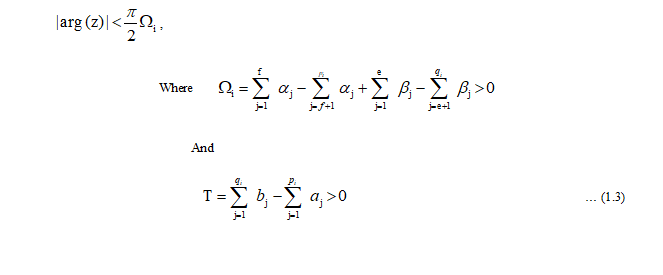
  Now following shorthand notations given by Srivastava and Daoust [6] denote the generalized Lauricella function of several complex variables.

        =    F                                              … (1.9)

            

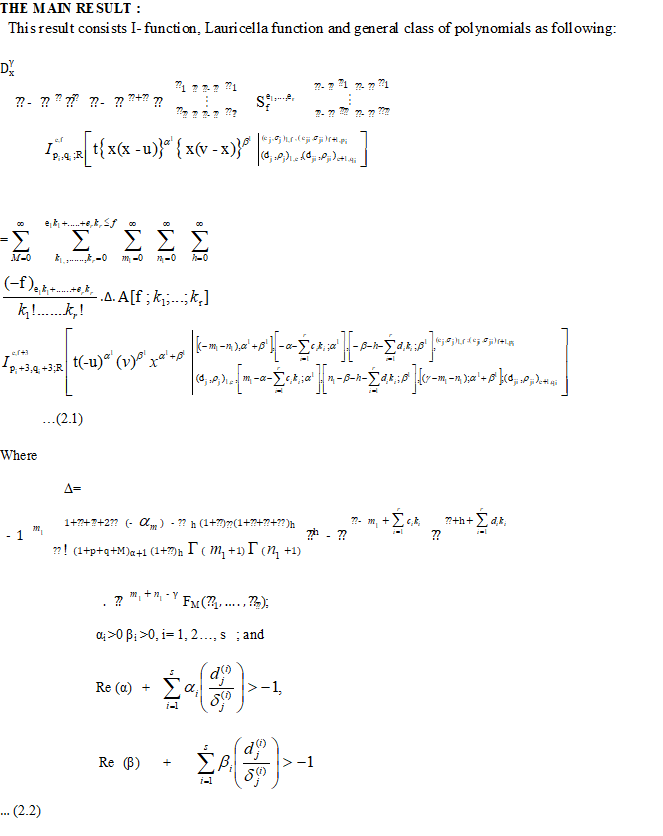
Proof: In order to prove (2.1), express the I-function in terms of Mellin-Barnes type of contour integrals by (1.1) and Lauricella function by (1.7) and general class of polynomials given by (1.4), then collecting the powers of (x-u) and (v-x). Finally making use of the result (1.6), we get the main result (2.1).

PARTICULAR CASES:

If we take R=1 in (1.1), then I-function breaks into well known Fox’s H-function and consequently there hold the following result:

 

 

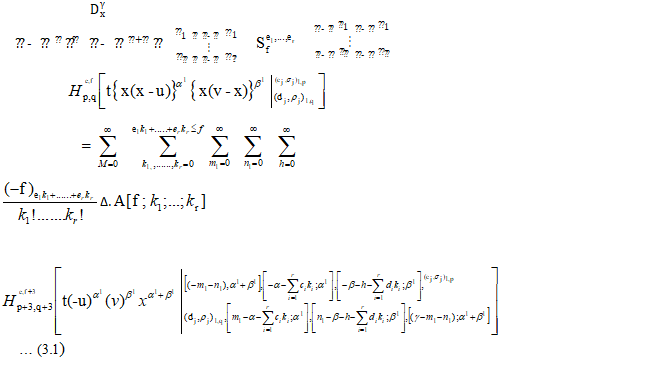
     Valid under the conditions surrounding (2.1)

  • If we take multivariable H-function in place of I-function in (2.1), then we have a known result obtained by  Chaurasia and Singhal [2] as following:

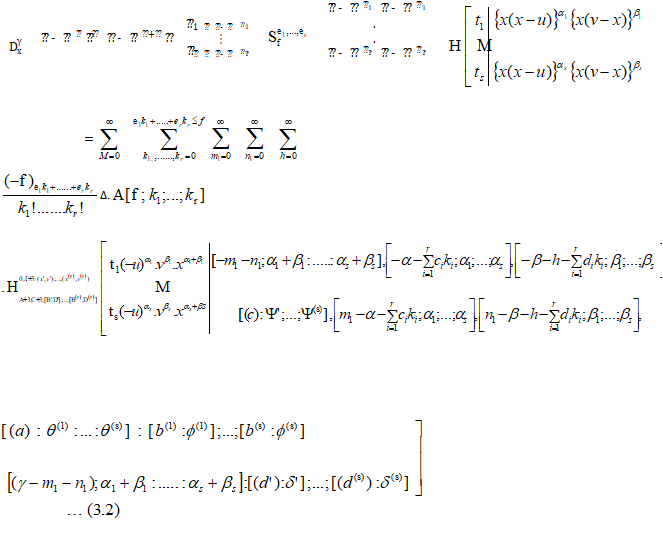
   Valid under the conditions surrounding (2.1)

Taking R=1 and replacing f→f1,….,fr in (2.1),

 we get a known result obtained by Chaurasia and Shekhawat [1].

Conclusion:

The main result derived here is of a very general Nature and hence encompass several cases of interest hitherto scattered in the literature.

REFERENCES:

  1. B.L. Chaurasia and A.S. Shekhawat, fractional derivative associated with the multivariable polynomials, Kyungpook math. J. 47 (2007),495-500.
  2. B.L. Chaurasia, fractional derivative of the multivariable polynomials, Bull. Malaysian Math. Sc. Soc.(second series), 26 (2003),1-8
  3. B. Oldham and J. Spanier, The fractional calculus, Academic Press New York, 1974.
  4. P.Saxena, The I-function, Anamaya Publishers, New Delhi (2008)
  5. Srivastava, H.M., A multilinear generating function for the Konhauser sets of bi-orthogonal polynomials suggested by the Laguerre polynomials, Pacific J. Math. 117, 183-191 (1985)
  6. M. Srivastava, and M.C. Daoust, certain generalized neuman expansions associated with the kempe’ de f’eriet function, Nederl.Akad.Wetensch Indag.Math., 31 (1969), 449-457.
  7. M. Srivastava, and M. Garg, some integrals involving a general class of polynomials and the multivariable H-function, Rev. Roumanie phys.,32 (1987), 685-692
  8. M. Srivastava, and S.P.Goyal, fractional derivatives of the H-function of several variables, J.Math. Anal. Appl. 112 (1985), 641-651.
  9. M. Srivastava, and R. Panda, certain expansion formulas involving the generalized Lauricella function, II comment math. Univ. St. Paul, 24 (1974), 7-14