Saif Ali
M.Tech Scholar, Department of CEIT, Suresh Gyan Vihar University, Jaipur
saif.ali@mygyanvihar.com
Manish Sharma
Associate Professor Department of CEIT, Suresh Gyan Vihar University, Jaipur
manish.sharma@mygyanvihar.com
Abstract: In this research work we are compressing the image using the mathematical tool principal component analysis and then recognize the image from the same data set by the model. First we will describe the basic concepts prevailing with principal component analysis. Then we will see that how principal component can be extracted from a given data set. Then we will go for sampling distribution of Eigen values and Eigen vectors. Then followed by model adequacy test, then we perform our task of image detection. The problem arises when we use high dimensionality space. Because in face or in 3d image, we have different eigen values or vectors and it can’t be fixed due to high dimensions as compared to 2d image. Hence, we use Principal Component Analysis(PCA).
Keywords: PCA, Eigen values, Eigen vectors, image compression. Dimension reduction
I. INTRODUCTION
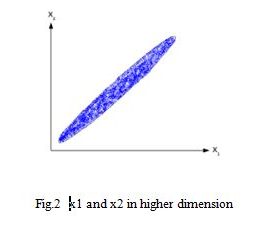
Data reduction technique it is extensively used and developed by developed by Hotelling H in 1933 and it is the data reduction is done with two prospective in mind, one is that lowered dimension, second one is orthogonality of the new dimensions. Orthogonality of the new dimensions. or transformed dimensions, which are basically PCS principal component[1]. So, let us now go for the very simple two dimensional plot for example, let our dataset is X, which basically composed of n x 2 that means m measurements on 2 variables. So, like this, so this one is variable and variable .then this one , . So, like this , then , like this, xn2 okay if we plot the data is here suppose this axis x1, this is x2. now, if we plot the data let us assume that the data is like this data plot looks like this if we compute the covariance matrix [2,3] of x. we will be getting as we are talking about data, so we have collected a sample in that sense we have to write this will be s11, s12 , s12, s22. So, 2 x 2 matrixes so this scattered diagram shows that there is a relationship between x1 and x2 so, if we calculate correlation matrix between for x, what will happen we will get certain correlation coefficient. This will be correlation matrix 2 x 2 we will find out that r12 to that will be as weknow, that correlation coefficient varies from- 1 to + 1 and here x2 and x1 the relationship is positive. So we will get it is a quite large value may be it may be almost = 0.9 here 0.90 getting Fig.2 and Fig.3. So, this is one aspect that we have taken two dimensional or regional
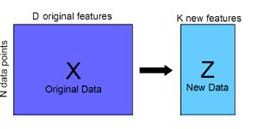
Fig.1 Block diagram of PCA

As a result, what will happen what are the advantages we will be getting from here advantages is, suppose we want to do a prediction model using multiple regression and my X variable, these are all independent variables. If are correlate then that ultimately leads to multicolinearity problem multicolinearity are there. So, under multicolinearity condition the regression model what you want to fit that y = f(x) linear model. This model will not be a good one, because under multico linearity it may not be possible to estimate the parameters.
II. METHODOLOGY
This paper validates the PCA algorithm on images for the first time where it has not been tested on images before. It also proposes a new learning method for face detection and recognition using the PCA algorithms.The PCA algorithm starts with the creation of a data set (in this paper, it contains training faces and ends with the projection of the data on the eigen space. A covariance matrix will computed for the data; in addition, the eigenvectors and eigen values of the covariance matrix will also obtained.
Working Principal
The following working steps are involved here.
- Collection of images
- Feature reduction by PCA
- Designing of model
- Training of model
- Testing of model
- PROBLEM FORMULATION
Face is a complex multidimensional structure and needs good computing techniques for recognition. Features extracted from a face are processed and compared with similarly processed faces present in the database. If a face is recognized it is known or the system may demonstrate a alikefeaturesaccessible in database else it is unknown. In observationorganization if a indefinitefeatures appears more than one time then it is stored in database for further recognition. The above steps can be used or image of any criminal identification
Face recognition is the challenge of classifying whose face is in an input image. With face recognition, we need an existing database of faces. Given a new image of a face, we need to report the person’s name. The problem arise when we use high dimensionality space. Because in face or in 3d image, we have different eigen values or vectors and it can’t be fixed due to high dimensions as compared to 2d image. Hence, we use Principal Component Analysis(PCA).The best low-dimensional space can be determined by best principal components. The major advantage of PCA is using it in eigenface approach which helps in reducing the size of the database for recognition of a test images. The images are stored as their feature vectors in the database which are found out projecting each and every trained image to the set of Eigen faces obtained. PCA is applied on Eigen face approach to reduce the dimensionality of a large data set.
IV. DATA DESCRIPTION
To understand the methodology adopted, we first understand our dataset and the variables.
Number of samples: 400
Height of each image: 64
Width of each image: 64
Number of input features: 4096
Number of output classes: 40
Working method
- Import Data through fetch_olivetti_faces from sklearn.datasets
- Slicing data by train_test_split from sklearn.model_selection library.
- Plotting the gray scale image of mean image and the images with unique id’s.
Principal Component Analysis(PCA) by
Eigen value, Eigen vectors
Covariance Matrix
K-Nearest Neighbour
V.RESULTS AND DISCUSSION
In this research work we are compressing the image using the mathematical tool princioal component analysis and then recognize the image from the same data set by the model. Here in this section we will discuss about our data set and the outcomes of our model.



Figure 6 is the collection of all images and then by algorithm we have design the mean image showing in the Fig.5. After applying the principal component we have reduce the size of the images by eliminating highly related components. Here we are losing approximately 20% information of the image.
At the time of detection we got the following result as shown in Fig.8 and Fig.9.

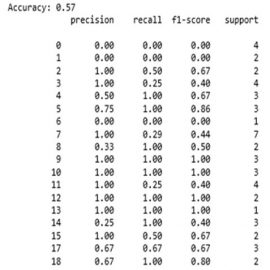
The accuracy of the system is 57 %
VI CONCLUSION
In this research work we are compressing the image using the mathematical tool princioal component analysis and then recognize the image from the same data set by the model. First we will describe the basic concepts prevailing with principal component analysis. Then we will see that how principal component can be extracted from a given data set. Then we will go for sampling distribution of Eigen values and Eigen vectors. Then followed by model adequacy test, then we perform our task of image detection. The problem arises when we use high dimensionality space. Because in face or in 3d image, we have different eigen values or vectors and it can’t be fixed due to high dimensions as compared to 2d image. Hence, we use Principal Component Analysis(PCA). After applying the principal component we have reduce the size of the images by eliminating highly related components. Here we are losing approximately 20% information of the image.The accuracy of the system is 57 %
REFERENCES
[1] L. I. Smith, “A tutorial on principal components analysis,”cs.otago.ac.nz/cosc453/studentutorials/principal components.pdf, February 2002. 537
[2] S.-F. Ding, Z.-Z. Shi, Y. Liang, and F.-X. Jin, “Information feature analysis and improved algorithm of pca,” in Machine Learning and Cybernetics, 2005. Proceedings of 2005 International Conference on, vol. 3, Aug 2005, pp. 1756–1761 Vol. 3, doi: 10.1109/ICMLC.2005.1527229. 537, 538, 539
[3] A. A. Alorf, “Comparison of computer-based and optical face recognition paradigms,” 2014. 538, 539, 543, 544, 545
[4] P. Kamencay, D. Jelovka, and M. Zachariasova, “The impact of segmentation on face recognition using the principal component analysis(pca),” in Signal Processing Algorithms, Architectures, Arrangements, and Applications Conference Proceedings (SPA), 2011, Sept 2011, pp. 1–4. 538
[5] B. C. Russell, W. T. Freeman, A. A. Efros, J. Sivic, and A. Zisserman, “Using multiple segmentations to discover objects and their extent in image collections,” in Computer Vision and Pattern Recognition, 2006 IEEE Computer Society Conference on, vol. 2, 2006, pp. 1605–1614.
[6] S. He, J. Ni, L.Wu, H.Wei, and S. Zhao, “Image threshold segmentation method with 2-d histogram based on multi-resolution analysis,” in Computer Science Education, 2009. ICCSE ’09. 4th International Conference on, July 2009, pp. 753–757. 538, 539
[7] I. Kim, J. H. Shim, and J. Yang, “Face detection,” Face Detection Project, EE368, Stanford University, vol. 28, 2003. 538, 539
[8] R. Gonzalez, R. Woods, and S. Eddins, Digital Image Processing Using MATLAB. Gatesmark, LLC, 2009, om/DIPUM-2E/dipum2e main page.htm, isbn: 978-0-9820854-0-0. 538, 540, 543
[9] M. Turk and A. Pentland, “Face recognition using eigenfaces,” in Computer Vision and Pattern Recognition, 1991. Proceedings CVPR ’91., IEEE Computer Society Conference on, Jun 1991, pp. 586–591, doi: 10.1109/CVPR.1991.139758, ISSN: 1063-6919. 538, 540, 541, 542, 543
[10]“Eigenfaces for recognition,” J. Cognitive Neuroscience, vol. 3, no. 1, pp. 71–86, Jan. 1991. [Online]. Available: http: //dx.doi.org/10.1162/jocn.1991.3.1.71 538, 540, 541, 542, 543
[11] W. Yang, C. Sun, L. Zhang, and K. Ricanek, “Laplacian bidirectional pca for face recognition,” Neurocomputing, vol. 74, no. 1, pp. 487–493, 2010. 539
[12] M. Al-Amin, “Towards face recognition using eigenface,” International Journal of Advanced Computer Science and Applications, vol. 7, no. 5, 2016. [Online]. Available: 2016.070505 539, 544
[13] Q. Fu, “Research and implementation of pca face recognition algorithm based on matlab,” in MATEC Web of Conferences, vol. 22. EDP Sciences, 2015. 539, 543, 544
[14] M. Abdullah, M. Wazzan, and S. Bo-Saeed, “Optimizing face recognition using pca,” arXiv preprint arXiv:1206.1515, 2012. 539
[15] S. K. Dandpat and S. Meher, “Performance improvement for face recognition using pca and two-dimensional pca,” in Computer Communication and Informatics (ICCCI), 2013 International Conference on, Jan 2013, pp. 1–5. 539, 544
