pp.6-9
Robert Kozma
University of Memphis
Abstract:-Neural cryptography deals with the problem of key exchange using the mutual learning concept between two neural networks. The two networks will exchange their outputs (in bits) so that the key between the two communicating parties is eventually represented in the final learned weights and the two networks are said to be synchronized. Security of neural synchronization depends on the probability that an attacker can synchronize with any of the two parties during the training process, so decreasing this probability improves the reliability of exchanging their output bits through a public channel. This work proposes an exchange technique that will disrupt the attacker confidence in the exchanged outputs during training. The algorithm is based on one party sending erroneous output bits with the other party being capable of predicting and removing this error. The proposed approach is shown to outperform the synchronization with feedback algorithm in the time needed for the parties to synchronize.
Keywords: Cryptography, mutual learning, neural cryptography, neural synchronization, tree parity machine.
I. INTRODUCTION
Neural networks (NNs) are able to solve so called non formalized problems or weakly formalized problems that requires learning process based on a real experimental data [1]. Supervised NNs models are trained on input/output pairs to achieve a certain task. This training is based on adjusting the initial randomized synaptic weights by applying a predefined learning rule. Two NNs having the same structure and different initial synaptic weights can do the same task if both are trained on the same input/output pairs while the final synaptic weights of the two networks need not be the same.
In fact this phenomenon is very interesting and can be modified to achieve another goal, i.e., the two networks have the same final weights. One way to do that is for the two networks to be presented with common input patterns while being trained on the output of each other instead of predefined target patterns. The applied learning rule needs to be so efficient that the two synaptic weight vectors of the two networks become close to each other and thus correlated. Hence, the final two weight vectors are almost identical. The correlation between the two weight vectors is also called the overlap. When the overlap is 100% (i.e. the two weight vectors are identical) it can be said that the two networks have synchronized with each other. An aim of cryptography is to transmit a secret message between two partners, A and B, while an attacker, E, who happens to access the communication channel will not be able to figure out the context of this message.
A number of methods have been introduced to achieve this goal [2][3][4][5]. In 1976 Diffie and Hellman developed a mechanism based on number theory by which a secret key can be exchanged by two parties over a public channel which is accessible to any attacker [2][3]. Alternatively, two networks trained on their outputs are able to achieve the same objective by means of mutual learning [6]. The most common model used in neural cryptography is known as the Tree parity Machine (TPM) since it keeps the state of the two parties secret, and thus it is more secure than using simple network. The aim of this work is to introduce a mechanism to improve the security of the mutual learning process, so that the attacker find it more difficult in listening to the communication between the two parties during the period in which they increase their weight vectors overlap. The paper is organized as follows. Section II presents an introduction to mutual learning in both a simple network and TPM. Section III shows a summary to most known attack against mutual learning. In section IV, a
brief explanation for neural synchronization with feedback [7] is presented. This method was developed to improve the security of the mutual learning process for the TPM model. In section V, the DTMP (Don’t Trust My Partner) with error prediction approach is proposed to improve the security of exchanging the two parties output bits. Section VI presents the possible break-on scenarios against the proposed method.
PAGE LAYOUT
II. INTRODUCTION SYNCHRONIZATION
between different entities is a known phenomenon that exists in different physical and biological systems. Synchronization in biological systems can be found in the behaviour of Southeast Asian fireiles [1], which is a biological type of phase synchronization of multiple oscillators. Also, another type of synchronizationexists in chaotic systems [2], where the
synchronization process in artificial neural networks (NNs) can be exploited in securing information transmission.
This paper presents three algorithms to enhance the security of neural cryptography in such a way that the attacker faces difficulties in trusting the transmitted information on the public channel. The proposed algorithms tamper with the listening process, which is the basic mechanism the attacker depends on to break into the system. This paper is organized as follows. Section II presents the mutual learning method for both simple networks and the TPM. Section III summarizes the most known attacks against mutual learning. In Section IV, the Do not Trust My Partner (DTMP) with error prediction approach is proposed to improve the security of exchanging the output bits of two communicating parties. Section V presents the possible breakin scenarios against the proposed method. In Section VI, the performance of the proposed algorithm is analyzed. Section VII presents simulation and experimental results for the DTMP algorithm. Section VIII introduces the Synchronization with Common Secret Feedback (SCSFB) algorithm as a modification for the synchronization with feedback algorithm. In Section IX, the two proposed approaches, i.e., DTMP and SCSFB, are combined to provide for additional secure communication.
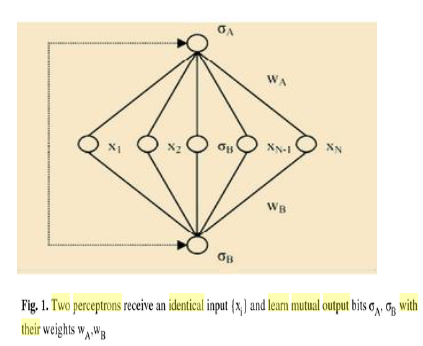
MUTUAL LEARNING IN TPMS The basic building block for the mutual learning process is a single perception. Fig. 1 depicts two communicating perceptions having different initial weights wA/B, and receiving the same random input x at every training step. The mutual learning process is based on exchanging output bits σ A/B between the two perceptions. The output σ is defined as
σi =sign(wT i .x) (i)
where
i ∈{A, B} and sign(n)= {1, for n ≥0; −1, otherwise
at the end of training step t, the weight vectors w are updated using the following learning rule [10]:
wA(t +1)=wA(t)+ η/ N x(t)σ B(t)ᴓ(−σ A(t)σ B(t))
wB(t +1)=wB(t)+ η/ N x(t)σ A(t) ᴓ(−σ A(t)σ B(t))
(ii)
where η is a suitable learning rate and ᴓ is the step function. Clearly, the weights will be updated only if the two output bits σ A and σ B disagree. After each weight update, the weight vectors of the two networks are kept normalized. If the learning rate exceeds a critical value ηc =1.816, the two weight vectors will satisfy the condition wA =−wB [10]. There are some restrictions on both the input and weight vector generation mechanisms in order to achieve full synchronization. The input pattern x has to be an N-dimensional vector with its components being generated from a zeromean unit-variance Gaussian distribution (continuous values). Also, the weight vector w is an N-dimensional vector with continuous components which should be normalized, i.e., ||wT.w=1||, since only normalized weights can synchronize.
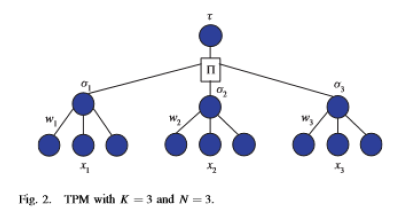
to synchronize with probability of 99% [10]. Consequently, another structure should be developed to hide the internal state of each party so that it cannot be reproduced from the transmitted information. A TPM structure that consists of K perceptions (Fig. 2), each with an output bit σk, is a candidate for improving the security of the mutual learning process and can be defined as
σk =sign(wT k .xk) (3)
The output of the TPM is
τ =π K k=1σk (4)
The continuous type of input and weight vector components are not suitable for cryptographic application. When only digital signaling (0s and 1s) is permitted, the input and weight components should be drawn from a discrete distribution rather than a continuous one. Bipolar input pattern sx∈{− 1,1}N and discrete weight vector wk, j ∈ {− L,−L +1,…L −1, L}N will be used here, where L is an integer value chosen by the designer to represent the synaptic depth of the network [10]. The two partners who need to share a common key will maintain two identical TPMs.
III. REFERENCES
[1] A. Pikovsky, M. Rosenblum, and J. Kurths, Synchronization: A Universal Concept in Nonlinear Sciences. Cambridge, U.K.: Cambridge Univ. Press, 2003.
[2] C.-M. Kim, S. Rim, and W.-H. Kye, “Sequential synchronization of chaotic systems with an application to communication,” Phys. Rev. Lett., vol. 88, no. 1, pp. 014103-1–014103-4, Dec. 2001.
[3] A. I. Galushkin, Neural Network Theory. New York: Springer-Verlag, 2007. [4] G. Pölzlbauer, T. Lidy, and A. Rauber, “Decision manifolds—a supervised learning algorithm based on self-organization,” IEEE Trans. Neural Netw., vol. 19, no. 9, pp. 1518–1530, Sep. 2008.
[5] I. Kanter, W. Kinzel, and E. Kanter, “Secure exchange of information by synchronization of neural networks,” Europhys. Lett., vol. 57, no. 1, pp. 141–147, 2002.
[6] W. Diffie and M. Hellman, “New directions in cryptography,” IEEE Trans. Inform. Theory, vol. 22, no. 6, pp. 644–654, Nov. 1976.
[7] A. J. Menezes, S. A. Vanstone, and P. C. Van Oorschot, Handbook of Applied Cryptography. Boca Raton, FL: CRC Press, 1996.
[8] B. Schneier, Applied Cryptography: Protocols, Algorithms, and Source Code in C, 2nd ed. New York: Wiley, 1995.
[9] W. Stallings, Cryptography and Network Security: Principles and Practice. Upper Saddle River, NJ: Pearson, 2002.
[10] E. Klein, R. Mislovaty, I. Kanter, A. Ruttor, and W. Kinzel, “Synchronization of neural networks by mutual learning and its application to cryptography,” in Advances in Neural Information Processing Systems 17, L. K. Saul, Y. Weiss, and L. Bottou, Eds. Cambridge, MA: MIT Press, 2005, pp. 689–696.
IV. AUTHORS INFORMATION
Ahmed M. Allam received the Graduate degree from the Computer and Systems Engineering Department, Ain Shams University, Cairo, Egypt, in 2008. He is currently pursuing the Masters degree in the same university. He joined Mentor Graphics Egypt, Cairo, as a Quality Assurance Engineer in 2008. In 2010, he joined a Synopsys partner, Swiftronix, Cairo, as a Digital Design and Verification Engineer. His current research interests include computational intelligence, digital design, quantum computing, cryptography, and quantum cryptography.
