Arpita Agrawal
Abstract— a motion blur is characterized by its point spread function (PSF) whose parameters are closely related to the motion. Estimating the PSF of a real-world motion-blurred image is an essential step in the restoration process. To estimate the PSF, some techniques assume that it is a spatially invariant square pulse, and extract the blur extent from the zero-crossings of the averaged power spectrum. Now days scholars have proposed new methods or improved blur detection algorithms which are based on blind de-convolution, point spread function (PSF) and many more. Motion blur retains some information about motion, based on which motion may be recovered from blurred images. This is a difficult problem, as the situations of motion blur can be quite complicated, such as they may be space variant, nonlinear, and local. A motion blur is characterized by its point spread function (PSF) whose parameters are closely related to the motion. Estimating the PSF of a real-world motion-blurred image is an essential step in the restoration process. To estimate the PSF, some techniques assume that it is a spatially invariant square pulse. The simplest motion blur is the space-invariant linear motion blur, which has been studied extensively. In practice, however, as motion can be quite complex, motion blurs can be much more complicated than this simple case. For example, the blur can be space-variant, nonlinear, local and multiple. The purpose of this paper is to extend the work area of already work done.
Keywords——Blur detection, blind de-convolution, point spread function
I.INTRODUCTION
Image deconvolution is a longstanding linear inverse problem with applications in remote sensing, medical imaging, astronomy, seismology, and, more generally, image restoration [1]. The challenge in many linear inverse problems is that they are ill-posed, i.e., either the linear operator does not admit inverse or it is near singular, yielding highly noise sensitive solutions. To cope with the ill-posed nature of these problems, a large number of techniques has been developed, most of them under the regularization [2, 3] or the Bayesian frameworks [4]. In addition to this a growing number of special issues and conferences are dedicated to remove the blur from the images which are taken and slightly blurred due to camera shake or low light condition of a scene. The articles are selected for this issue present new approaches and ideas for the detection of blur. Blur is the degradation of sharpness and contrast of an image which cause loss of high frequency
- For the de-blurring process we generally apply some algorithm which estimate the blur and then recover the image into its possible and probable condition. Several methods are used to recover the blur from the image and some method are used which are sometimes hard-coded and sometime user configurable. In which we use a function called point spread function (PSF).
A motion blur is characterized by its point spread function (PSF) in which the parameters of PSF are closely related to the motion. The simplest motion blur is the space-invariant linear motion blur, which has been studied extensively. In practice, however, as motion can be quite complex, motion blurs can be much more complicated than this simple case. For example, the blur can be space-variant, nonlinear, local and multiple.
Blur detection method can be applied as initial stage for de-blurring when the machine vision of manufacturing line is out of focus or due to rapid movement of the inspected product. Some of the restrictions are there in the blur detection technique that’s why many researchers research so many algorithms to detect more blur from the image [5]. Some of them are belongs to variant methods, point spread functions and de-convolution methods. Based on analysis on the past researches on the blur detection methods, blur detection can be classified in to some categories, which are:
1.De-blurring using Gaussian method
2.De-blurring using blind de-convolution method
3.Using motion de-blurring method
For linear and shift-invariant motion-blurring, the blurred image g(x, y) may be written as the convolution of the scene f(x, y) and the point spread function (PSF) h(x, y):
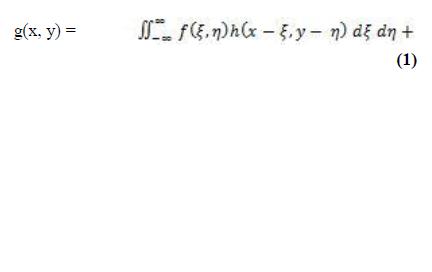
where n (x, y) represents additive noise. A Fourier trans- form of Eq. (1) gives
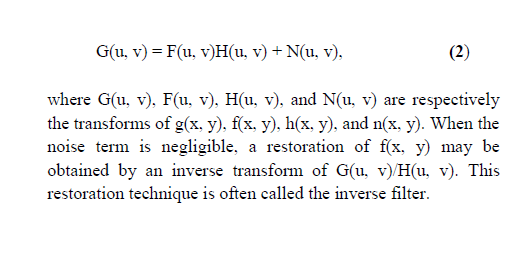
II.RELATED WORK
Most algorithms to compute TV-based estimates are developed on the continuous domain. These algorithms fall into two main categories. Restoration of blurred images is a vital problem especially in tracking and identification of criminals. The available image can be used to identify a human face or a moving vehicle’s number plate taken in hit and run situation or in a bomb blast site. To restore a blurred image successfully, blurring function needs to be estimated accurately. Blurring function is referred to as Point Spread Function (PSF) which is the response of an imaging system to a point source or it can be said as the impulse response of a focused optical system [1]. Existing system used a single hardcoded method to de-blur a natural image. Technologies used in this method are more common but the mathematical approaches are sometimes changed with some more configurations. Technologies which are used in exiting system are motion blue remover, Gaussian blur remover and blind estimation PSF. Along with these techniques only a single technique is used which is generally hard coded and not permitted to change by user.
III ADOPTED METHODS
Blind single-image de-blurring is a method used to restore a sharp image from an image blurred by camera shakes or object motion under low light conditions. Generally blur occurred due to motion or low light conditions. To solve this problem many researchers do necessary researches and work using blurred images and its mathematic approaches. From the various challenges of photography, one is motion blur. Blur problems are generated from relative motion between a camera and a picture during exposure. While blur can be reduced by using a shorter exposure, this comes at an unavoidable trade-off with increased noise. So blur can be removed computationally. This is the main motive of this research. Now the question is that how to remove blur.
In the complete procedure of this de-blurring the main challenge is to estimate the exact figure of natural blurred images. Another difficulty is that algorithm needs to distinguish the correct image–blur pair from incorrect ones that can also adequately explain the blurred image. De-convolution is also difficult because the algorithm needs to restore high frequency image contents attenuated by blur. In this dissertation, we address a few aspects of these challenges.
IV.COMPLETED WORK
This paper work started with the approach of estimating the blur parameters using the algorithms discussed below. The algorithm aims at determining the Blur parameters such as length of blur in pixels and the angle of blur in degrees. This algorithm used for estimating the blur parameters, de-blurring of the image using the estimated parameters, its limitations and the proposed Efficient De-blurring Algorithm for natural images.
V.RESULTS
From these results, we deduce that when restoring a real-world motion-blurred image, some exploratory restorations may be carried out using assumed-PSFs, in or- der to determine the shape and blur extent of the true- PSF, guided by the characteristics of the exploratory restorations obtained. The estimated true-PSF may then be used for the final restoration. On the basis of the results of the last section, we may conclude that a square-pulse PSF is not a suitable assumed-PSF for exploratory restoration.
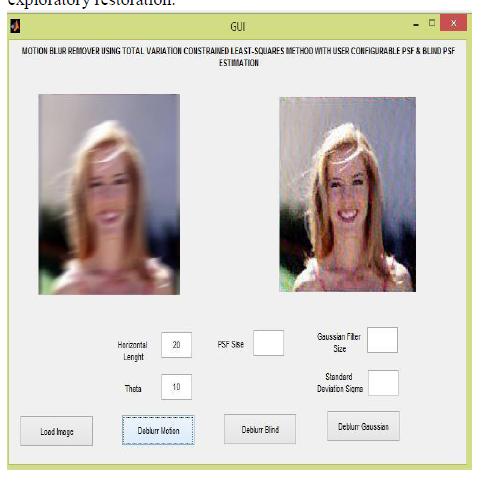
Fig: 1 A restoration obtained with measures of de-blurring using motion constraints.
According to these results we deduce that when restoring a real-world motion-blurred image, some exploratory restorations may be carried out using assumed-PSFs, in order to determine the shape and blur extent of the true- PSF, guided by the characteristics of the exploratory restorations obtained. The estimated true-PSF may then be used for the final restoration. On the basis of the results of the
On the basis of the above observations, we propose the following strategy for the exploratory restoration of images which have been motion-blurred with an unknown PSF:
- Use a forward-ramp for the first trial restoration.
- If the restoration from (1) shows a smeared-out scene terminated in a strong, clear ghost, use a reverse- ramp for a second trial restoration.
- If the restoration from (1) or (2) shows a ghost, we may assume a square-pulse or trapezoid true-PSF. Mea- sure the displacement of the ghost from the true scene to obtain the blur extent of the true-PSF. Using a square pulse with this estimated blur extent, another restoration is carried out.
- If the restoration from (3) shows ringing, try a trape-zoid PSF with the same estimated blur extent. Use a forward- or a reverse-trapezoid PSF depending on whether a forward- or a reverse-ramp was found more appropriate in steps (1) and (2).For more demanding applications, we may use the above procedure to establish the overall structure of the true-PSF and then experiment with fine variations in PSF shapes to obtain a really high quality restoration. An advantage of the above procedure is that the true-PSFs may be determined to reasonable accuracy even if they are not spatially invariant.
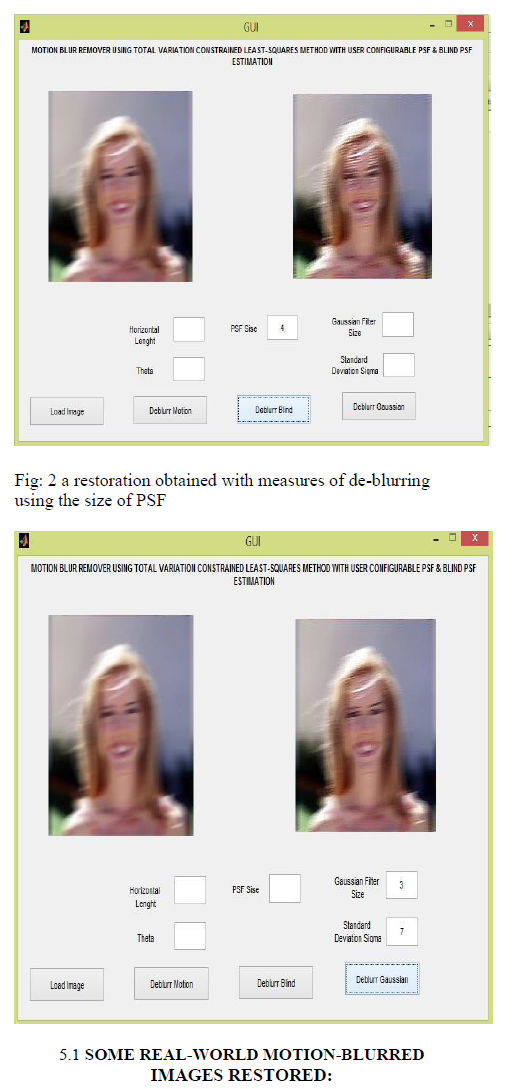
In this section we apply the restoration procedure to the major three techniques of de-blurring. Blurring was caused by panning the camera when the shutter was being released. The images were digitized with a monochrome video camera with back illumination.

In Fig. 3, the text is badly blurred, but the holes and pins are clearly visible. Figure 4 show the image restored using motion de-blurred process. Pin numbers and texts are clearly visible.

VI.SUMMARY AND CONCLUSION
Summary:
When we took a picture sometimes it shakes due to some motion or low light. Due to this blurring of image occurs. To address this problem, some researches do their efficient work on de-blurring dynamic scenes and prepare an approach that commonly requires accurate motion segmentation. To explore the existing system’s approach we differentiate it with the previously done work and the new approach which we are doing. Till yet the de-blurring is done by applying several methods of de-blurring but single approach in single time. We are applying a hardcoded system according to which user can configure the approach for de-blurring.
Estimating the PSF of a real-world motion-blurred image is an essential step in the restoration process. This paper addresses the problem of blind motion de-convolution without assuming that the entire image undergone the same blur. In this we apply the procedure of de-blurring with several techniques
Conclusion:
Image de-blurring or restoration have wide applications, from consumer photography, e.g., remove motion blur due to camera shake, to radar imaging and tomography, e.g., remove the effect of imaging system response. This tutorial has presented the image degradation and restoration model. The relative sub-models and model estimation have also been introduced. Although the concept of image restoration is relatively simple, the actual implementation is somewhat difficult, as prior knowledge of the degradation function and noise model is often not possible. The research includes several concepts of image processing and tools of MATLAB to de-blur the blurred image which is blurred by camera shake. In this research many techniques of de-blurring is used which can be of many procedures. The operated system works in a very fine way and work on the estimation of PSF which is point spread function. Our approach takes advantage of both images to produce a high quality reconstructed image.
VII ACKNOWLEDGMENT
It is my pleasure to express my hearty gratitude to my teacher and guide, Mr. sachin jain, (Assistant Professor), Faculty of Engineering, Department of Computer Science & Engineering, Suresh Gyan Vihar University, Jaipur, who inspired and initiated me to prepare this research despite his busy academic schedule. He has always been kind enough to spare his valuable time and thought in giving necessary guidance. His rich experience as an academician helped me in understanding this topic clearly. Finally, words are insufficient to express my profound sense of gratitude to my parents whose motivation and blessing always provides me with great strength.My especial thanks to Mr. Dinesh Goyal (associate professor), SGVU, Jaipur who helped me for this research.

