Role of Process Algebra In Qualitative Modeling Of Multi Agent Systems
1Ruchi Dave, 2Devesh Bandil
1Suresh Gyan Vihar University, 2Suresh Gyan Vihar University
Jaipur, India, Jaipur, India
1ruchi.davey@gmail.com, 2drdevesh.bandil@mygyanvihar.com
Abstract—Process Algebra is a parallel operator as we know. It is very important in order to test non-trivial properties of the system. Process polynomial mathematics or Process Algebra as we all know is a scientific structure or a framework where system behavior is expressed as algebraic terms, upgrading the accessible strategies for control, Utilizations and applicability of procedure variable based math exist in assorted fields, for example, security based frameworks, arrange conventions, System conduct or behavior by and large comprises of procedures and information. Procedures are the control components for the control of information. These forms or processes can be dynamic and active or running, whereas the information that is associated is static and also passive . Framework conduct will in general be made out of a few procedures that are executed simultaneously, where these procedures trade information so as to impact each other’s behavior. The aim of this paper is to study the usefulness of Process Algebra in qualitative modeling of multi agent system and value of Process Algebra in subjective displaying of multi operator framework or multi agent system modeling.
Index Terms—BAS, Building Automation System, Modeling Petri nets, Multi agent System
- INTRODUCTION
Procedure Algebra or as most of us call it Process Algebra is an equal administrator which is never really down the framework into simultaneous segments so as to test non-inconsequential properties of the framework .This generic term comprises the study of communicating processes in an algebraic fashion. In this approach, atomic actions, algebraic operations and equation axioms are used to describe and analyze processes. Typically, a distributed system or concurrent protocol can be described as the concurrent execution of a number of elementary sub processes, possibly employing
synchronous or asynchronous communication .The external behavior of such a system can be obtained by abstracting from internal activity, and can then be matched against a ‘specification’ of the process This allows the verification of global correctness of the system .Process algebra provides an algebraic framework for such correctness issues.
- Background and Literature
A process algebra is a formal description technique for complex computer systems, especially those with communicating, concurrently executing components. However, the advent of time
sharing, computer networking, parallel computing, object oriented programming, and graphical user interfaces has stressed and complicated the whole model. As per the growth that we have seen in past the computers are more for communication and connectivity rather than Computation and research and the best thing happened is that it is now the necessity of the time.
If we start by the name as what we mean by a “Process” and “Algebra” then the definition would be
Definition 1. A group has a signature (G, *, u-1 ) with the laws
– a * (b * c) = (a * b) * c
– u * a = a = a * u
– a * a −1 = a −1 * a = u
A group is any mathematical structure with operators satisfying the group axioms. So whenever we wish to express behavior using process algebra we take axiomatic approach for studying the behavior of the group and definitely a group is a model of the equation theory[1]
If we go back checking the history of development of Process Algebra we find that in 1980s, process algebras such as Tony Hoare’s CSP (Calculus of Sequential Processes) [2]Bergstra and Klop’s ACP (Algebra of Communicating Processes) [3] . J.C.M. Baeten and J.A. Bergstra. Real time process algebra. Formal Aspects of Computing, 3(2):142–188, 1991, and Robin Milner’s CCS (Calculus of Communicating Systems)[4]were introduced to give a richer theoretical model, using concurrency and synchronization as the fundamental primitives of a theory of interacting systems were introduced to give a richer theoretical model, using concurrency and synchronization as the fundamental primitives of a theory of interacting systems. Later, Milner introduced 15 the π-calculus [88A. Pnueli. The temporal logic of programs. In Proceedings 19th Symposium on Foundations of Computer Science, pages 46–57. IEEE, 1977.] which models mobile communication between processes using channel names: processes communicate by sending and receiving channel names, which makes it possible to represent dynamic networks of interacting processes, and gives a model rich enough to include both concurrent communication and sequential computation (in particular, to encode the λ-calculus [86]). To give a basic example, in the π-calculus we can describe a system with processes/agents such as, A
A(y) , a.0 + y(x).A(x)
A number of different process algebras have been developed – ACP[15] CCS and TCSP and all of them have discussed “Compositional modeling” which provides explicit representations for modeling assumptions to support automatic formulation of models.Hence we have observed that Process algebras provide a small number of constructs for building larger systems up from smaller ones.For example CCS, contains six operators in total, including ones for composing systems in parallel and others for choice and scoping.
Further as the theory that existed is the theory of Petri nets conceived by Petri starting from his thesis in 1962 [84] C.A. Petri. Kommunikation mit Automaten. PhD thesis, Institut fuer Instrumentelle Mathematik, Bonn, 1962.We can distinguish three main styles of formal reasoning about computer programs, focusing on giving meanings to programming languages.
- Operational semantics : A computer program is modeled as an execution of an abstract machine. A state of such a machine is a valuation of variables, a transition between states is an elementary program instruction. Pioneer of this field is McCarthy[17]. J. McCarthy. A basis for a mathematical theory of computation. In P. Braffort and D. Hirshberg, editors, Computer Programming and Formal Systems, pages 33–70. North-Holland, Amsterdam, 1963.
- Denotational semantics: It is more abstract than operational semantics, computer programs are usually modeled by a function transforming input into output. Most well-known is the work of Scott and Strachey [6]. In J. Fox, editor, Proceedings Symposium Computers and Automata, pages 19–46. Polytechnic Institute of Brooklyn Press, 1971.
- Axiomatic semantics :The emphasis is put on proof methods proving programs correct. Central notions are program assertions, proof triples consisting of precondition, program statement and post condition, and invariants. Floyd [7] Then, the question was raised how to give semantics to programs containing a parallel operator.
Behavioral reasoning via equivalences and preorders
Procedure algebras additionally include the utilization of conduct relations as a methods for relating various frameworks given in the polynomial math. These relations are normally equivalences, which catch a thought of ”same conduct”, or preorders, which further captures the ideas of ”refinement”. In a procedure arithmetical way to deal with framework confirmation, one ordinarily composes two details (I) call it SYS, catches the plan of the genuine framework and (II) call it SPEC, portrays the framework’s ideal “elevated level” conduct. One may then set up the accuracy of SYS as for SPEC by indicating that SYS carries on “equivalent to” SPEC (if utilizing identicalness) or by demonstrating that it refines SPEC (if utilizing a preorder). Setting up the rightness of SYS as for SPEC should be possible in a grammar arranged way or in a semantics-situated way. In the previous case, an axiomatization of the conduct connection of decision is utilized to show that one articulation can be changed into the other by means of syntactic controls. In the last case, one can advance straightforwardly to the meaning of the conduct connection, and to the operational semantics of the two articulations, to show that they are connected. In specific cases, e.g., when SYS and SPEC are “limited state”, check, be it linguistic structure based or semantics-based, can be completed.
Benefits of Algebric Approach of modeling:
The advantages to an algebraic approach are the following.System designers need learn only one language for specifications and designs.Related processes may be substituted for one another inside other processes. This makes process algebras particularly suitable for the modular analysis of complex systems, since a specification and a design adhering to this specification may be used interchangeably inside larger systems. Procedures might be limited concerning the proportionality connection before being dissected; this occasionally prompts significant degrees of improvement in the presentation of check schedules. Procedure mathematical framework portrayals can likewise be confirmed utilizing model checking 9[3], a method for determining if a named progress framework fulfills a rightness property given as a fleeting rationale recipe. Model checking has appreciated extensive accomplishment in application to equipment structures. Progress is currently being seen in other application areas, for example, programming and convention verification. Process polynomial math can be seen as a speculation of the traditional hypothesis of formal dialects and automata[10] concentrating on framework detail and conduct as opposed to language acknowledgment and age. Procedure variable based math additionally epitomizes the standards of cell automata 11 cells getting contributions from neighboring cells and afterward making fitting move – while including a thought of programmability: no determinism, dynamic topologies, advancing cell conduct, and so forth. Procedure polynomial math lays the basis for a thorough framework structure belief system, offering help for particular, check, execution, testing and other life-cycle-basic exercises. Enthusiasm for process polynomial math, be that as it may, stretches out past the framework plan field, to regions, for example, programming language structure and semantics, multifaceted nature hypothesis, constant programming, and execution displaying and examination.
Modal Logic Verses Process Algebra
Ever since the early 1970’s modal languages have been used as description languages for structures such as labeled transition systems. Modal formulas are evaluated locally, at a single state inside a labeled transition system; the mechanism for evaluating formulas does not take one outside the system, but instead it forces certain moves along the restricted patterns described by the modal operators. Another special feature of modal languages is that they are relatively constrained fragments of classical languages such as first-order logic.In general, modal languages avoid the quantificational power of classical languages whereas Process Algebra comprises the study of concurrent (communicating) processes in an algebraic fashion In this approach, atomic actions, algebraic operations and equation axioms are used to describe and analyze processes Typically, a distributed system or concurrent protocol can be described as the concurrent execution of a number of elementary sub processes, possibly employing synchronous or asynchronous communication The external behavior of such a system can be obtained by abstracting from internal activity, and can then be matched against a ‘specification’ of the process This allows the verification of global correctness of the system Process algebra provides an algebraic framework for such correctness issue. The most obvious difference is that modal formulas are evaluated inside the transition system, whereas process-algebraic terms are interpreted by a structure as a whole One might call modal logic an internal language of labeled transition systems and process algebra an external one.[16]
Key Principles of Quantitative Modeling :
With this three important functions are there which is essential for qualitative modeling. are(i)Discretization (ii) Relevance(iii)Ambiguity never to be skipped in the designing of models.Most software systems are now de facto concurrent and distributed, and are expected to interact with components and exploit services that are dynamically found in the network also software systems are becoming “always-on” entities that cannot be stopped, restored, and maintained in the traditional way. So to keep up the time multiagent systems are the only solutions for current softwares.
Multi Agent System: A multi-agent system (MAS or “self-organized system”) is a computerized system composed of multiple interacting intelligent agents. Multi-agent systems can solve problems that are difficult or impossible for an individual agent or a monolithic system to solve.[18] Intelligence may include methodic, functional, procedural approaches, algorithmic search or reinforcement learning.[19]
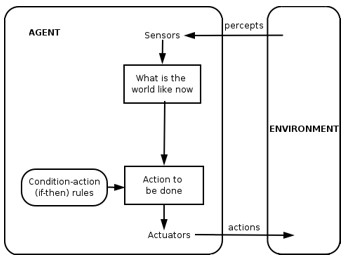
Fig(1) A Simple Agent
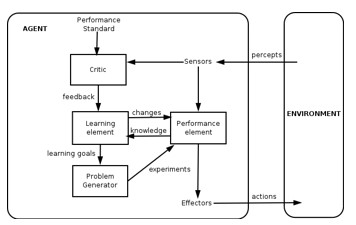
Fig.(1.1) A Learning Agent
As the two figures fig(1) and fig (1.1) depicts the concept of agent oriented system where the first system is a simple agent oriented system and second is a learning agent oriented system which is smart and updating itself about the System and the environment as a whole.Likewise if we understand that in a system Specialists in multi-agent framework (MAS) are by and large social and coordinate with other specialists within the Multi agent arrange to attain more common objectives such as social objectives of the Multi agent system.
MAS can give a run-time back to those frameworks which requires self-organization and adjustment towards the arrangement of maintainable administrations.
Conclusion : This paper presents the Process Algebras and its usefulness to construct a formal establishment for a number of fundamental concepts of computer science such as forms, interaction, and disseminated computing. On the other hand, multiagent frameworks opens the area of social sciences , brain research and so on. A multiagent system may specific sort of disseminated framework.Essentially composed of a (conceivably open) set of independent specialists, a highlights other sorts of substances and deliberations, such as assets of different sorts (sensors,actuators, etc)
References :
- Handbook of Process https://basics.sjtu.edu.cn/~yuxin/teaching/Concurrency/AHistory.pdf(Accessed online)
- R. Milner. Bigraphical reactive systems. In K.G. Larsen and M. Nielsen, editors, Proceedings CONCUR ’01, number 2154 in LNCS, pages 16–35. Springer Verlag, 2001
- J.C.M. Baeten and J.A. Bergstra. Real time process algebra. Formal Aspects of Computing, 3(2):142–188, 1991,
- C.A. Petri. Introduction to general net theory. In W. Brauer, editor, Proc. Advanced Course on General Net Theory, Processes and Systems, number 84 in LNCS, pages 1–20. Springer Verlag, 1980
- R. Milner, A Calculus of Communicating Systems, Lecture Notes in Comput. Sci. 92, Springer-Verlag (1980). R. Milner, A Calculus of Communicating Systems, Lecture Notes in Comput. Sci. 92, Springer-Verlag (1980).
- D.S. Scott and C. Strachey. Towards a mathematical semantics for computer languages. In J. Fox, editor, Proceedings Symposium Computers and Automata, pages 19–46. Polytechnic Institute of Brooklyn Press, 1971.
- R.W. Floyd. Assigning meanings to programs. In J.T. Schwartz, editor, Proceedings Symposium in Applied Mathematics, Mathematical Aspects of Computer Science, pages 19–32. AMS, 1967.
- M. Hennessy and G.D. Plotkin. Full abstraction for a simple parallel programming language. In J. Becvar, editor, Proceedings MFCS, number 74 in LNCS, pages 108– 120. Springer Verlag, 1979.
- L. Aceto, Z. Esik, W.J. Fokkink, and A. Ing´olfsd´ottir, editors. ´ Process Algebra: Open Problems and Future Directions. BRICS Notes Series NS-03-3, 2003. 3. L. Aceto, W.J. Fokkink, and C. Verhoef. Structural operational semantics. In [25], pp. 197–292, 2001.
- R. Alur, C. Courcoubetis, N. Halbwachs, T.A. Henzinger, P.-H. Ho, X. Nicollin, A. Olivero, J. Sifakis, and S. Yovine. The algorithmic analysis of hybrid systems. Theoretical Computer Science, 138:3–34, 1995.
- S. Andova. Probabilistic Process Algebra. PhD thesis, Technische Universiteit Eindhoven, 2002.
- Handbook of Knowledge Representation Edited by F. van Harmelen, V. Lifschitz and B. Porter © 2008 Elsevier B.V. All rights reserved DOI: 10.1016/S1574-6526(07)03009-X
- C.A. Petri. Introduction to general net theory. In W. Brauer, editor, Proc. Advanced Course on General Net Theory, Processes and Systems, number 84 in LNCS, pages 1–20. Springer Verlag, 1980.
- https://www.cs.ox.ac.uk/people/michael.wooldridge/pubs[12] Handbook of Knowledge Representation Edited by F. van Harmelen, V. /tosem2003.pdf
- J. A. Bergstra and J.W. Klop, Process algebra for synchronous communication. Inform, and Control 60 (1/3) (1984), 109-137.
- Modal Logic and Process AlgebraA Bisimulation Perspective edited by Alban Ponse, Maarten de Rijke, and Yde Venema
- J. McCarthy. A basis for a mathematical theory of computation. In P. Braffort and D. Hirshberg, editors, Computer Programming and Formal Systems, pages 33–70. North-Holland, Amsterdam, 1963.
- “A Multi Agent-Based System for Securing University Campus: Design and Architecture – IEEE Conference Publication”. 2019-12-17. doi:10.1109/ISMS.2010.25
- “Multi Agent Systems – an overview”. ScienceDirect Topics. 2016-01-01.Retrieved 2020-01-23
